Предмет: Геометрия,
автор: Леха19971995
Точка О - центр вписанной окружности треугольника АВС. Докажите, что угол АОВ=90 градусов + 1/2 угла АСВ.
Приложения:
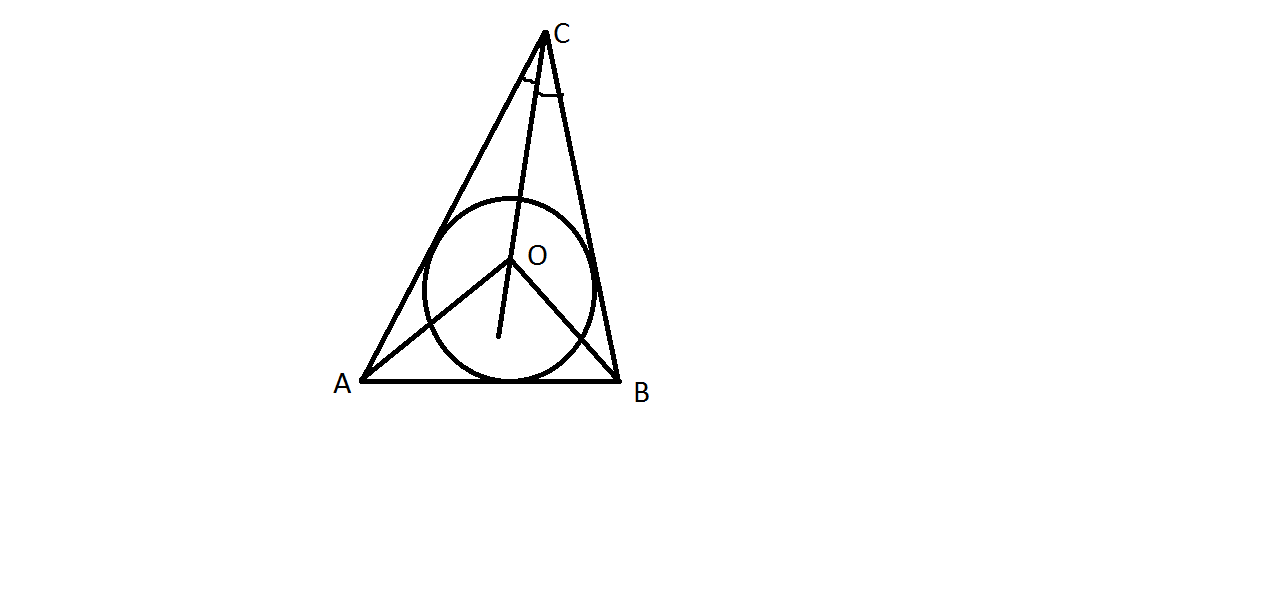
Ответы
Автор ответа:
0
Центр вписанной окружности лежит на пересечении биссектрис, поэтому
угол ОАВ=1/2 * угол А
угол ОВА=1/2*угол В
Сумма углов треугольника равна 180 градусов
В треугольнике АОВ (используя сумму для углов треугольника АВС)
угол АОВ=180 градусов - угол ОАВ-угол ОВА=180 градусов -(1/2 * угол А+1/2 * угол В)=90 градусов +90 градусов-(1/2 * угол А+1/2 * угол В)=90 градусов+1/2(180 градусов -угол А-угол В)=90 градусов +1/2*угол С=90 градусов +1/2 угла АСВ
Доказано
Похожие вопросы
Предмет: Алгебра,
автор: N0pichky
Предмет: Литература,
автор: olgakim30061984
Предмет: Математика,
автор: reunovadasha2000
Предмет: Математика,
автор: BEYBIK1
Предмет: Химия,
автор: ГидроПонка228