Question

Найдите расстояние между высотой правильного тетраэдра,ребро которого равно 10 корней из 3, и средней линией его боковой грани Я нашла высоту, она равна 15 Ответ должен получиться:2,5 см

Answer 1

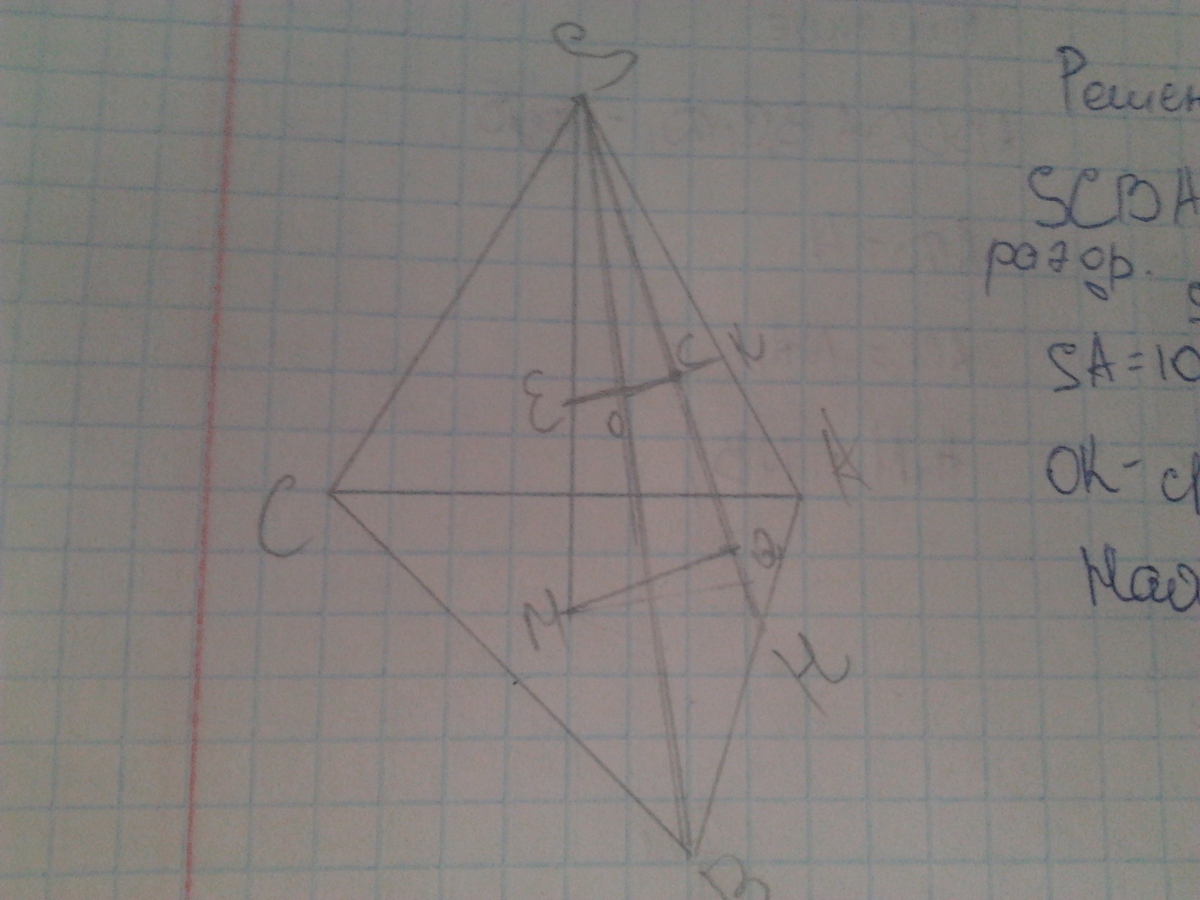
Расстояние от центра описанной около основания этого тетраэдра окружности до грани - перпендикуляр к этой грани.

На рисунке - это отрезок ОК.

Центр описанной около правильного треугольника окружности ( а грани правильного тетраэдра - правильные треугольники) лежит на пересечении высот треугольника на расстоянии одной трети высоты от стороны.

Найдем высоту треугольника по формуле
h=a√3):2, а так как а=1,то 
h= √3):2

ОМ=√3):2):3=√3):6

Так как все грани правильного тетраэдра равны, 
SM равна h=√3):2

Расстояние КО будем находить из прямоугольного треугольника SОМ
Применим теорему:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.

Здесь этот катет - ОМ

 

ОМ²=МК·SM

(√3):6)²=МК·(√3):2)

 

МК=3/36:(√3):2)=6/36):√3=1/6√3

 

ОК²=МО²-КМ²

ОК²=3/36 -1/108=9/108-1/108=8/108=2/27=6/81

ОК =√(6/81)=√6):9

  Вложения