Предмет: Геометрия,
автор: stiki
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60. Высота пирамиды равна 18. Найдите объем пирамиды.
Ответы
Автор ответа:
3
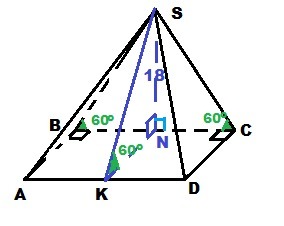
Дано: SABCD - пирамида; ABCD - прямоугольник
(SBC)⊥(ABCD); ∠SCB = ∠SBC = ∠SKN = 60°
SN = 18
Найти: V пирамиды
Решение:
ΔSNC - прямоугольный
tg 60° = SN/NC ⇒ NC = SN/tg 60° = 18/√3 = 6√3
ΔSBN = ΔSNC = ΔSKN - по общему катету и углу 60° ⇒
KN = BN = NC = 6√3
BC = 2NC = 2*6√3 = 12√3
Объем пирамиды

V=1296 кв.ед.
(SBC)⊥(ABCD); ∠SCB = ∠SBC = ∠SKN = 60°
SN = 18
Найти: V пирамиды
Решение:
ΔSNC - прямоугольный
tg 60° = SN/NC ⇒ NC = SN/tg 60° = 18/√3 = 6√3
ΔSBN = ΔSNC = ΔSKN - по общему катету и углу 60° ⇒
KN = BN = NC = 6√3
BC = 2NC = 2*6√3 = 12√3
Объем пирамиды
V=1296 кв.ед.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Askeladd17
Предмет: Биология,
автор: stasdra4ov10
Предмет: История,
автор: malichenkodanil
Предмет: Алгебра,
автор: kott5
Предмет: Алгебра,
автор: kott5