Question

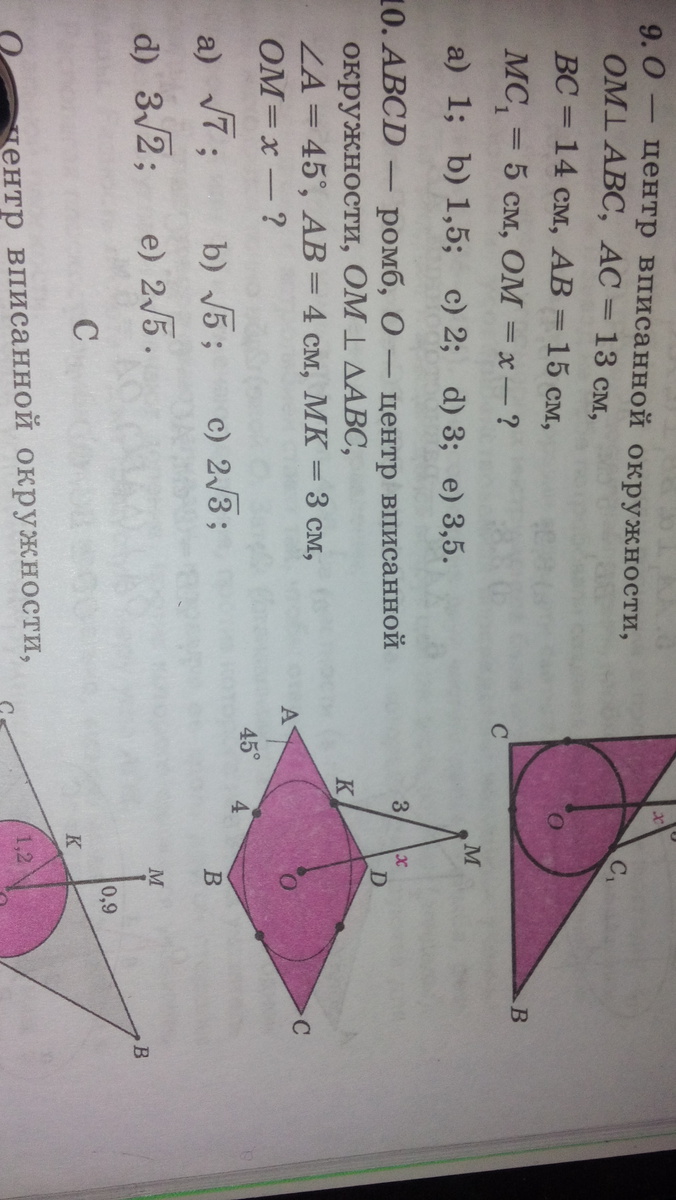
АВСД-ромб, О-центр вписанной окружности,ОМ перпендикулярно треугольнику АВС, угол А=45град,АВ=4см, МК=3см,ОМ=? помоги пожалуйста, срочно....

Answer 1

Проведем высоту DP: треугольник ADP - равнобедренный, потому как <DAP = 45 градусов, <ADP = 90 - 45 = 45 градусов. По теореме синусов: DA/sin(BPA) = DE/sin(DAP), 4/sin(90) = DP/sin(45), 4/1 = DP/sqrt(2)/2 (DP поделить на корень из двух деленный на два). DP = два корня из двух. DP - высота ромба. Радиус вписанной окружности равен половине этой высоты. R = OK = DP/2, что равно корень из двух. Из прямоугольного треугольника OMK: из теоремы Пифагора: OM^2 = MK^2 - OK^2, OM^2 = 9 - 4,  OM^2 = 5, OM = sqrt(5).
Ответ: ОМ равно корень из пяти.