Question

Най­ди­те боль­шую диа­го­наль ромба, сто­ро­на ко­то­ро­го равна 11√3 , а ост­рый угол равен 60°.

Answer 1

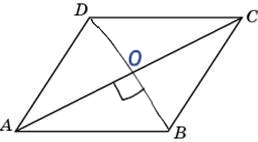
ABCD - ромб

По свойству ромба: диагонали ромба точкой пересечения делятся пополам, взаимно перпендикулярны и являются биссектрисами его углов  ⇒  AO = OC , BO = OD , AC⊥BD , ∠DAC = ∠BAC = ∠DCA = ∠BCA , ∠ADB = ∠CDB = ∠ABD = ∠CBD

∠DAC = ∠BAC = ∠A/2 = 60°/2 = 30°

В ΔADO: катет, лежащий против угла в 30°, равен половине гипотенузы ⇒ OD = AD/2 = 11√3/2

По теореме Пифагора:

AD² = AO² + OD²

AO² = AD² - OD² = (11√3)² - (11√3/2)² = 363 - (363/4) = (4•363 - 363)/4 = 3•363/4 = 3•121•3/4

AO = 3•11/2 = 33/2

Значит, АС = 2•АО = 2•(33/2) = 33

ОТВЕТ: 33