Предмет: Геометрия,
автор: k0sach
В окружность радиуса 5 корней из 5 вписан прямоугольный треугольник так, что один из катетов вдвое ближе к центру чем другой. Найдите длину большего катета.
Ответы
Автор ответа:
0
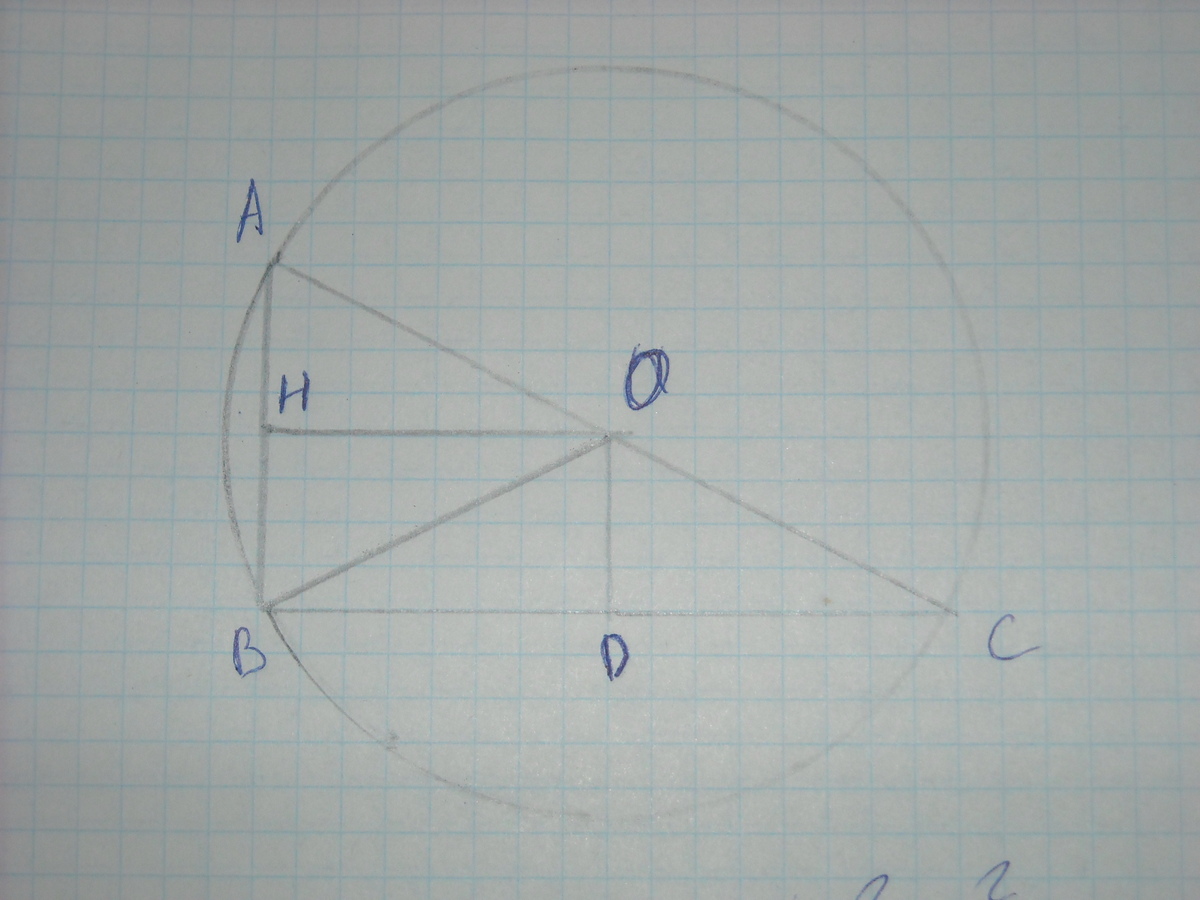
(Чертеж во вложении)
Опустим из цетра окружности перпендикуляры к катетам, получится прямоугольник ОДВН
(т к ОН перпендикулярна НВ и ВД перпендикулярна НВ, ОД перпендикулярна ВД)
В нем диагональ ОВ равна радиусу окр., а стороны ОН и ОД расстояния от центра до катетоа => ОН=2ОД, пусть НВ=ОД=х, ВД=ОН=2х,
Рассмотрим прямоугольный треугольник ОДВ по т пифагора
Но нам известно, что перпендикуляр проведенный из центра окружности к катетам вписанного в нее треугольника делит катеты на 2 => ВС=2*ВД=20
АВ=НВ*2=10
Ответ 10, 20
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: extravibe
Предмет: Физика,
автор: makhabbatlpl
Предмет: Физика,
автор: b0nes1337pocan123
Предмет: Математика,
автор: Artem334