Предмет: Алгебра,
автор: 707m
в геометрической прогрессии сумма первого и третьего членов равна 10, а сумма второго и четвертого членов равна -5 . найдите сумму геометрической прогрессии.
Ответы
Автор ответа:
0
.......................................................................
Приложения:
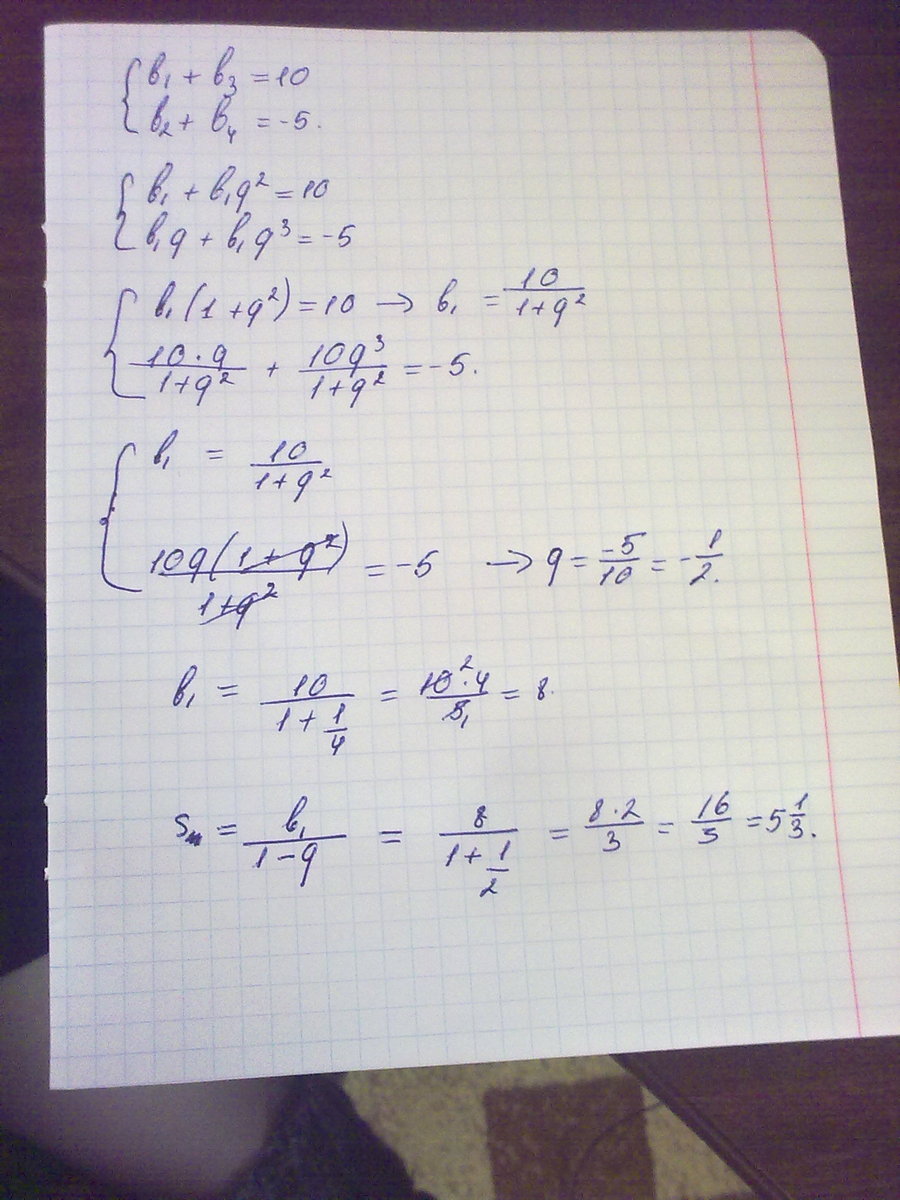
Автор ответа:
0
Ответ:
Объяснение:
b₁ + b₃ = 10
b₂ + b₄ = -5
распишем эти равенства
b₁ + b₁ · q² = 10 ⇒ b₁ (1 + q²) = 10 ⇒ b₁ = 10 : (1 + q²) (1)
b₁ · q + b₁ · q³ = -5 ⇒ b₁q (1 + q²) = -5 (2)
Подставим (1) в (2)
10 · q · (1 + q²) : (1 + q²) = -5
10q = -5
q = -0.5
b₁ = 10 : (1 + (-0.5)²) = 8
Поскольку эта прогрессия, если считать, что количество членов не ограничивается четырьмя, является бесконечной убывающей геометрической прогрессией, так как |q| < 1, то сумма такой прогрессии равна
Похожие вопросы
Предмет: Физика,
автор: vkim25713
Предмет: География,
автор: ogankovadara
Предмет: Литература,
автор: valeriezdradovskaya
Предмет: Математика,
автор: Kseniamylove
Предмет: История,
автор: Алисия999