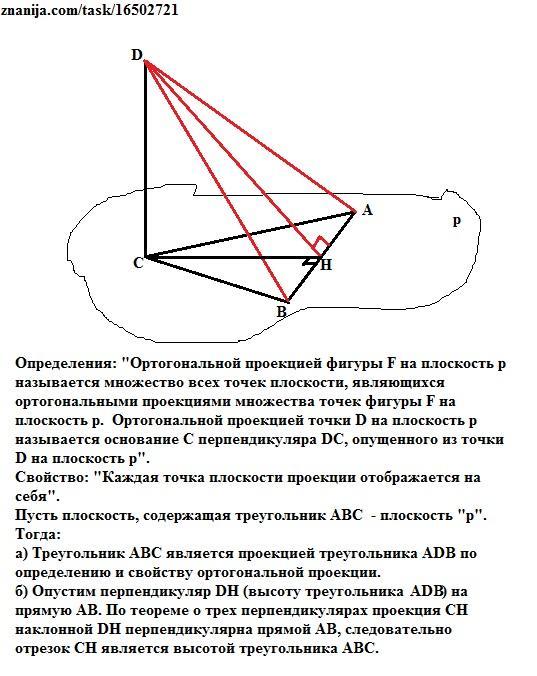
Прямая CD перпендикулярна к плоскости треугольника АВС. Докажите, что: а) треугольник АБС является проекцией треугольника ABD на плоскость АБС; б) если СН — высота треугольника АБС, то DH — высота треугольника ABD
Ответы
Ответ:
Доказательства в объяснении.
Объяснение:
Определения: "Ортогональной проекцией фигуры F на плоскость p называется множество всех точек плоскости, являющихся ортогональными проекциями множества точек фигуры F на плоскость p. Ортогональной проекцией точки D на плоскость p называется основание C перпендикуляра DC, опущенного из точки D на плоскость p".
Свойство: "Каждая точка плоскости проекции отображается на себя".
Пусть плоскость, содержащая треугольник АВС - плоскость "р".
Тогда:
a) Треугольник АВС является проекцией треугольника ADB на плоскость "р" по определению и свойству ортогональной проекции, так как точка С является проекцией точки D на плоскость р, а точки А и В лежат в плоскости р, то есть отображаются сами на себя.
б) Опустим перпендикуляр СH (высоту треугольника АВC) на прямую АВ. По теореме о трех перпендикулярах наклонная DH перпендикулярна прямой АВ, так как проекция СН этой наклонной перпендикулярна прямой АВ. Следовательно, наклонная DН является высотой треугольника АВD. Что и требовалось доказать.