Question

В треугольнике АВС АВ=ВС. Медианы треуголника пересекаются в точке О, ОА=5,ОВ=6. Найдите площадь треугольника АВС

Answer 1

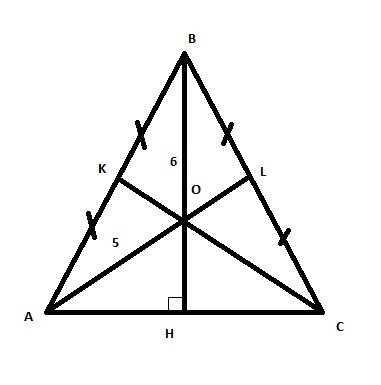
AB=BC. AL , CK , BH - медианы .

S(ABC)-?

Будем решать за формулой $S=frac{1}{2}*b*h_b$ , Медиана , проведенная к основанию  АС  является высотой ( по свойству равнобедренного треугольника ).

Медианы треугольника делятся в соотношении 2 : 1 , считая от вершины. Тогда, OB = 2x = 6 . Отсюда x = 3 см. OH = 3 см.

Из ΔAHO ( ∠AHO = 90 ° ) за Т. Пифагора :

$AH=sqrt{AO^2-OH^2}\AH=sqrt{5^2-3^2}\AH=sqrt{25-9}\AH=sqrt{16}\AH=4$ см.

AC = 2*AH=2*4=8 см. BH = BO + OH = 6 + 3 = 9 см.

Найдём площадь:

$S=frac{1}{2}*8*9=4*9=boxed{36}$

Ответ: 36 см².