Question

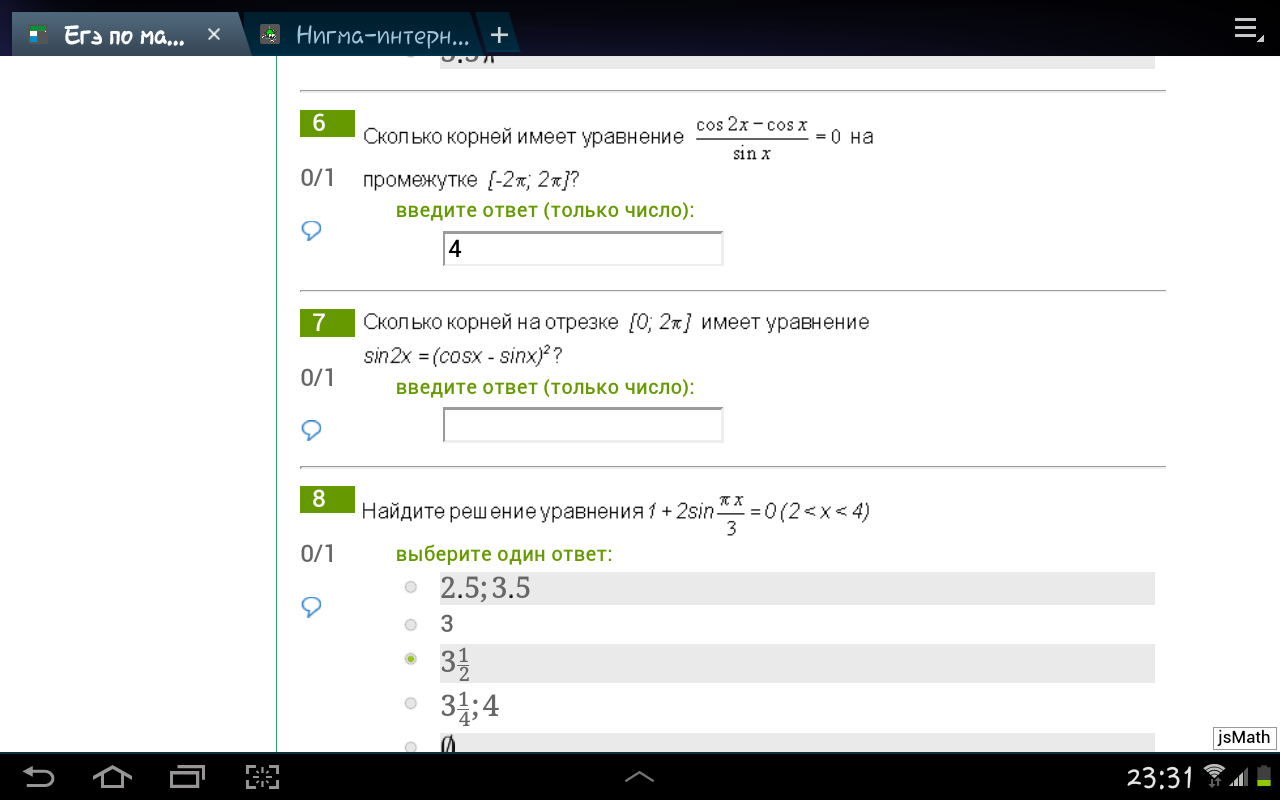
сколько корней имеет уравнение на отрезке [0;2п]   sin(2x)=(cos(x)-sin(x))^2

Answer 1

sin2x= 2*sinx*cosx

(cos(x)-sin(x))^2 = cox^2x -2*sinx*cosx+ sin^2x =  -2*sinx*cosx+1

 2*sinx*cosx=  - 2*sinx*cosx+1

 4*sinx*cosx = 1 

sinx*cosx = 1/4

(sin2x+sin0)/2 = 1/4

sin2x+sin0 = 0.5

sin 2x = 0.5

2x = (-1)в степени n*П/6+Пn

x =  (-1)в степени n*П/12+Пn/2

 

n = 0  x = П/12

n = 1  x = -П/12+П/2 = 5П/12 

n = -1 x = -П/12-Пn/2 = не удовл. условию

n = 2  x = П/12+П = 7П/12

n= 3 х= -П/12+3П/2 = 17П/12

 n= 4 n = 2  x = П/12+2П =  не удовлетворяет условию

 

ответ : 3 корня

 

Answer 2

$sin2x=1-sin2x\2sin2x=1\sin2x=frac{1}{2}\2x_1=frac{pi}{6}+2pi n;x_1=frac{pi}{12}+pi n;n in Z\2x_1=frac{5pi}{6}+2pi n;x_1=frac{5pi}{12}+pi n;n in Z$

Ответ :4 решения