Question

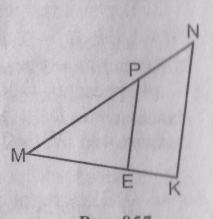
1. Дано: РЕ || NK, MP = 8, MN= 12, ME = 6. (рисунок)

Найти: а) МК; б) РE : NK; в) SMEP : SMKN.

2.  AВС АВ =12см, BС=18см, B = 70°, а в MNK MN= 6 см, NK = 9 см, 

 N= 70°. Найдите сторону АС и угол С треугольника ABС, если MK= 7 см, 

K= 60°. 

3. Отрезки АB и CD пересекаются в т. O так, что  ACO = BDO, 

АО : ОВ = 2:3. Найдите периметр треугольника АСО, 

если периметр треугольника BOD равен 21 см.

4*. В трапеции ABCD (AD и ВС основания) диагонали пересекаются в точке О, 

SАОД = 32 см2, SВос = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см.

Answer 1

№1 по теореме Фалеса

МN/МP = MK/ME

12/8=MK/6

MK= 9

 

МP/МN =PE/NK

8/12=PE/NK = 2 : 3

 

№2

Треугольник АВС подобен треугольнику MNK по второму признаку подобности (по двум пропорцианильным сторонам и равному углу между ними)

AB/MN = BC/NK=12/6=18/9=2 - коэф.подобности,

Значит AB/MN= AC/MK , MK= 12 x 7/6=14

В подобных треугольниках соответствующие углы равны.

угол С =60, угол А =50

№3

треугольник АОС подобен треугольнику ОДВ по первому признаку подобности (по двум равным углам)

Периметры подобных треугольников относятся как соответствующие стороны -

Периметр АОС : периметру ВОД = АО : ОВ=2 :3,

Периметрр АОС = периметр ВОД х 2 /3= 21 х 2/3=14