Question

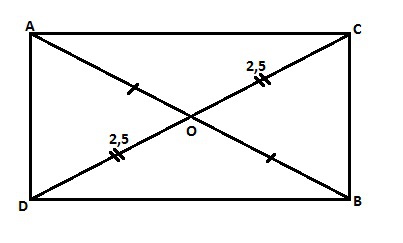
отрезки AB и CD пересикаются в точке О: OB=OC, OA=OD, CD=5см.Найдите АВ. Докажите, что треугольники DOB и COA равны.

Answer 1

Отрезок АВ делится на два отрезка: АО и ОС. Тогда, АВ=АО+ОС.
ОА=ОD - по условию, ОС=ОВ - по условию. Следовательно, АВ
=ОD+ОВ. А СD=ОD+ОВ. -> AB=CD=5 см.
Рассмотрим треугольники DOB и COA. Угол АОС и DOВ - вертикальные углы, а они равны, тогда, угол AOC= угол DOB.
ОА=ОD - по условию, ОС=ОВ - по условию. Тогда,треугольники DOB и COA равны по первому признаку равенства треугольников.