Предмет: Алгебра,
автор: Olga45m
Помогите решить, очень нужно.
Приложения:

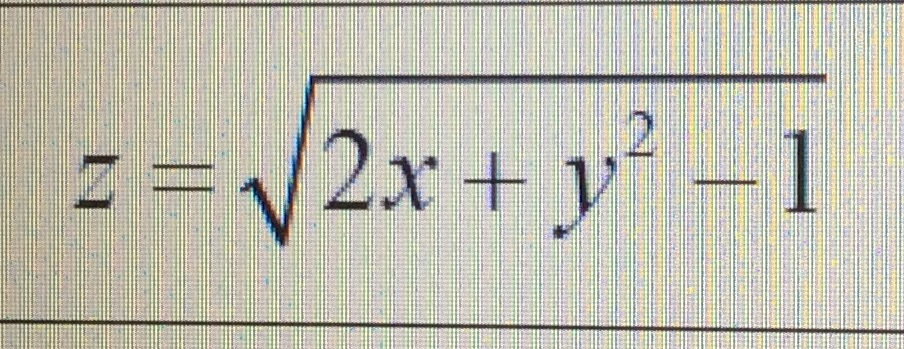
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: videoatomnyj
Предмет: Математика,
автор: sarkoma
Предмет: Математика,
автор: passedq6
Предмет: Химия,
автор: uzilonuzilonuzilon