Question

помогите, пожалуйста, решить

1/2(cos^2(x)+cos^2(2x))-1=2sin(2x)-2sinx-2sinx*sin^2(x)

Answer 1

sin x + cos x =1

2 sin x - 2 sin x +2 

Answer 2

1/2(cos^2(x)+cos^2(2x))-1=2sin(2x)-2sinx-2sinx*sin^2(x)

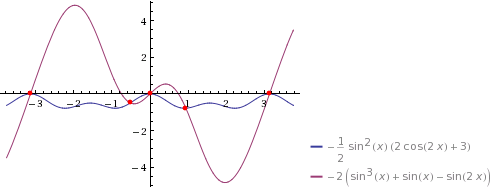
-1/2sin^2(x) (2cos(2x)+3)=-2(sin^3(x)+sin(x)-sin(2x))

1/2(cos^2(x)+cos^2(2x)-2)=-2(sin^3(x)+sin(x)-sin(2x))

4sin(2x)+sin(x) (sin(3x)+2(sin(x)+cos(2x)-3))=0