Предмет: Геометрия,
автор: konstantinvoro
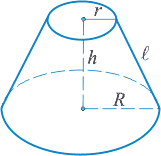
длина диаметра оснований и образующий равны соответственно 10,22,20 найти высоту и площадь полной поверхности Усечённого конуса
Ответы
Автор ответа:
0
r= 10/2 =5
R= 22/2 =11
l=20
H= √(l^2 - (R−r)^2)
H= √(20^2 - (11−5)^2) = √(400 - 36) = √364 = 2√91 ~ 19,078
Полная площадь поверхности усеченного конуса:
S= π(R^2 + r^2 + l(R+r))
S= π(11^2 + 5^2 + 20(11+5)) = π(121+25+320) = 466π ~ 1463,982
R= 22/2 =11
l=20
H= √(l^2 - (R−r)^2)
H= √(20^2 - (11−5)^2) = √(400 - 36) = √364 = 2√91 ~ 19,078
Полная площадь поверхности усеченного конуса:
S= π(R^2 + r^2 + l(R+r))
S= π(11^2 + 5^2 + 20(11+5)) = π(121+25+320) = 466π ~ 1463,982
Приложения:
Автор ответа:
0
У вас формула полной поверхности не верна
Автор ответа:
0
Ну, давайте смотреть: площадь основания с радиусом r = πr²; площадь основания с радиусом R = πR²; площадь боковой поверхности = πl (R+r). Площадь полной поверхности - сумма всего этого. Выносим π за скобки. Где ошибка?
Автор ответа:
0
Sполн=πr(e+r) Мне такую дали формулу
Автор ответа:
0
Это формула площади полной поверхности _целого_ конуса.
А в задаче площадь полной поверхности _усеченного_ конуса.
А в задаче площадь полной поверхности _усеченного_ конуса.
Автор ответа:
0
Я уже обнаружил ошибку для усечённого вот она Sбок + Пr^2+ Пr1^2
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Обществознание,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним