Question

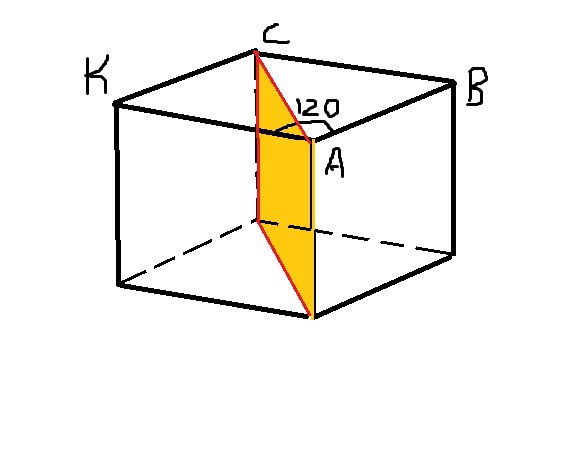
Основание прямой призмы - параллелограмм со сторонами 8 и 15 см и углом 120 градусов. Боковая поверхность призмы имеет площадь 460 кв. см. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
(если можно, пожалуйста, с рисунком и подробным объяснением)

Answer 1

Боковая поверхность прямой призмы равнапроизведению периметра основания на высоту. Периметр основания равен(8+15)*2=46 см. Боковая поверхность 460 см². 460/46=10 см - это высота.
Площадь сечения равна произведению диагонали АС на высоту.
Диагональ АС ищем по теореме косинусов: 
АС² = АВ²+ВС²-2*АВ*АС*cosB.  ∠B=60°, cosB=0.5.
AC² =8²+15²-2*8*15*0.5 289-120=69.
AC=√69. Площадь сечения равна √69 * 10 = 10√69см²