Question

Помогите решить задачу. В кубе abcda1b1c1d1 найдите угол между плоскостью a1bd и плоскостью, проходящей через середины его рёбер AB, BB1, B1C1,C1D1, D1D,DA.

Answer 1

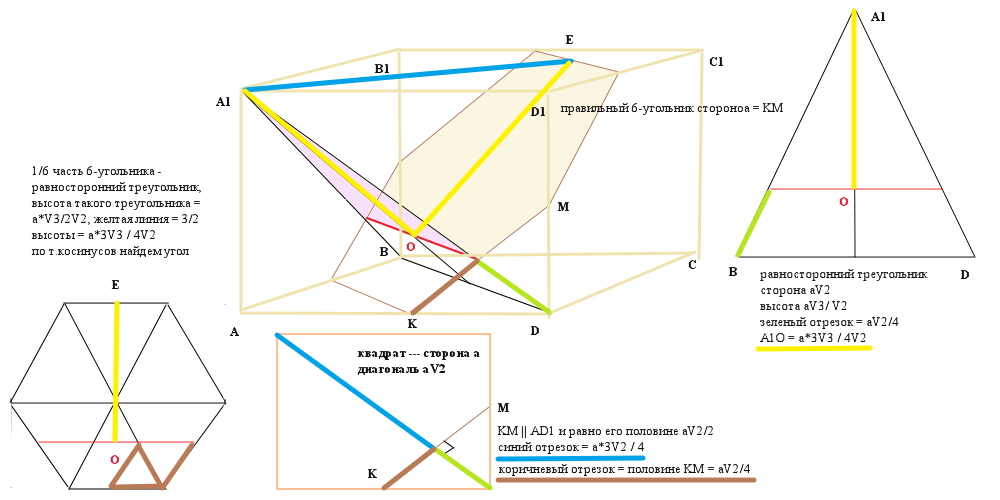
искомый угол A1OE

по т.косинусов A1E^2 = 2*A1O^2 - 2*A1O^2*cosA1OE = 2*A1O^2*(1-cosA1OE)

cosA1OE = 1 - A1E^2 / 2*A1O^2 = 1 - (18a^2 / 16) / (2*27*a^2/32) =

1 - (9*a^2 / 8) * (16 / (27*a^2)) = 1 - 9*16 / (8*27) = 1 - 2/3 = 1/3

угол A1OE = arccos(1/3) это примерно 70 градусов