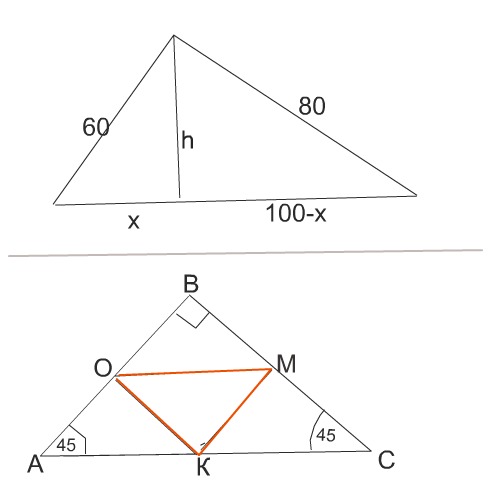
Катеты CK и CP прямоугольного треугольника KCP соотстветственно равны 60см и 80см. Найдите высоту этого треугольника,опущенную на гипотенузу.
В прямоугольном треугольнике с углом в 45 градусов и гипотенузой 8 см,проведены средние линии. Найти периметр треугольника,образованного средними линиями.
Ответы
Найдем гипотенузу по теореме Пифагора. Она равна 100 см
Высота делит гипотенузу на два отрезка
Пусть меньший будет х, тогда больший -100-х
Треугольник делит на два меньшего размера. Из каждого выразим высоту по теореме Пифагора:
h²= 60²-х²
h²=80²- (100-х)²
Приравняем значение высоты ( высота одна и та же и ее длина одна и та же в обоих случаях)
80²-(100-х)²=60²-х²
80²- 100²+200х-х ²=60²-х²
80²- 100²+200х =60²
200х=10000-6400+3600
200х=7200
х=36
Можно высоту найти по теореме Пифагора из одного из треугольников, на которые она поделила исходный. Но можно иначе.
Вспомним теорему:
Высота прямоугольного треугольника, проведенная из вершины прямого угла,
есть среднее пропорциональное между отрезками, на которые делится
гипотенуза этой высотой.
h²=36*64
h=6*8=48 см
-----------------
2) Сделаем рисунок, хотя вполне можно и без него обойтись.
Треугольник ОМК - образован средними линиями треугольника АВС, в котором углы при основании АС равны 45 градусам и поэтому он равнобедренный.
Эти треугольники подобны по свойству углов при пересечении параллельных прямых секущей. (Средняя линия - параллельна сходственной стороне и равна ее половине).
Коэффициент подобия этих треугольников 1/2.
Найдем катеты исходного треугольника.
Квадрат гипотенузы равен сумме квадратов катетов прямоугольного треугольника.
8²=2а²
а²=64:2=32
а=4√2 - длина каждого катета исходного треугольника
(2*4√2+8)
Периметры подобных фигур относятся как их стороны.
Р=(2*4√2+8)=8(√2+1)
Периметр получившегося треугольника равен половине периметра исходного и равен:
р= 8(√2+1):2=4( √2+1)
/