Question

доказать что a параллельно b решите пожалуйста

Answer 1

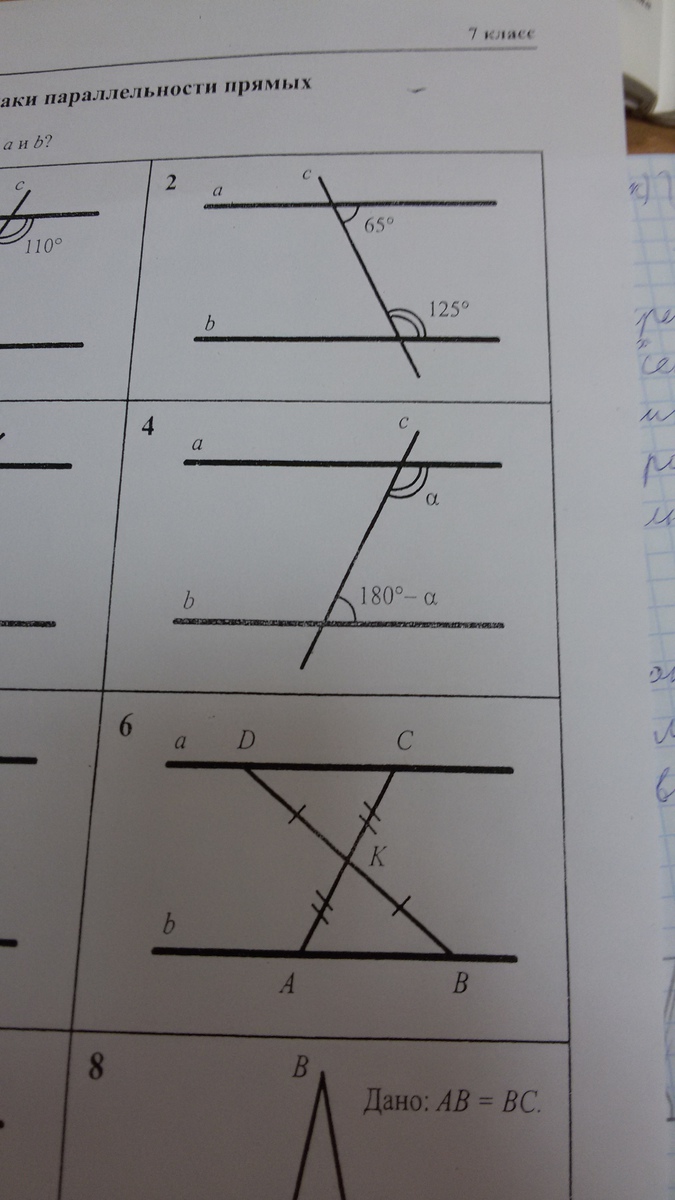
2. Сумма внутренних односторонних углов равна 65°+125°=190°, значит прямые "а" и "b" НЕ ПАРАЛЛЕЛЬНЫ (признак параллельности - сумма внутренних односторонних углов при параллельных прямых =180°).
4. Прямые "а" и "b" параллельны, так как α+(180°-α)=180°.
6. Треугольники АКВ и DKC равны по двум сторонам (АК=КС и ВК=KD дано) <DKC=<AKB как вертикальные. В равных треугольниках против равных сторон лежат равные углы. <A=<C, а это накрест лежащие углы при прямых "а" и "b" и секущей АС. Значит прямые "а" и "b" параллельны по признаку.
8. треугольник АВС равнобедренный (АВ=ВС - дано). Значит <BAC=<BCA=80°. <KAP=<BAC-<PAC=80°-40°=40°.
Треугольник АКР равнобедренный, так как АК=КР (дано), значит
<APK=<KAP=40° (углы при основании равнобедренного треугольника).
Итак, <APK=<PAC=40°, а это накрест лежащие углы при прямых "а" и "b" и секущей АР. Следовательно, прямые "а" и "b" параллельны по признаку.