Question

Умоляю!помогите с теорией вероятности (теорема Байеса)
Производится один выстрел по плоскости ,на которой расположены две цели : 1 и 2. Вероятность попадания в цель 1 равна 0,8 в цель 2 равна 0,9.После выстрела получено известие ,что попадания в цель 1 не произошло .Какова теперь вероятность того,что произошло попадание в цель 2?

Answer 1

Расчет ведем такой.
Выстрел всего один, поэтому вероятность выбора мишени р1(1)=р1(2) = 0,5.
Вероятность попадания  р2(1)=0,8   р2(2)= 0,9
Вероятность промаха q2(1)=1-0.8=0.2, q2(2)=0.1.
Вероятность попасть КУДА-НИБУДЬ  p(А)=0,5*0,8 + 0,5*0,9 =
0,40 + 0,45 = 0,85 - попасть. Вероятность МИМО - q(A) =1-p(A) = 0.15.
По Байесу - вероятность попасть во 2-ю мишень р(2)= 0,45/0,85=0,5294
в 1-ю мишень р(1) = 0,40/0,85=0,4706
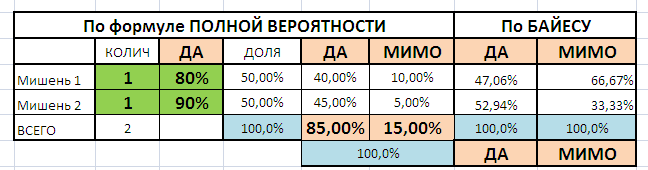
Расчеты сведены в таблицу.

Answer 2

В таблице как бы два выстрела, но вероятность 0,5. Можно поставить и 0,5+0,5 выстрела