Предмет: Геометрия,
автор: natan231099
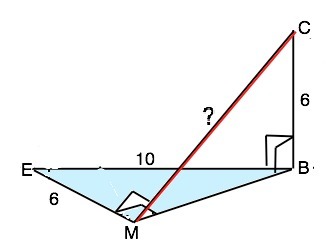
Прямоугольный треугольник MBE (∢M=90°) находится в плоскости α. BE=10 см, а ME=6 см. К этой плоскости проведён перпендикуляр CB длиной 6 см.
Вычисли расстояние от точки C до стороны треугольника ME.
Плиз, объясните :3
Ответы
Автор ответа:
0
Отношение катета МЕ и гипотенузы ВЕ=3:5, значит, второй катет⊿ МВЕ (египетского) равен 8 см (и по т.Пифагора ВМ=8 см). По условию ВС - перпендикуляр к плоскости треугольника, следовательно, перпендикулярен ВЕ и ВМ. Расстояние от точки до прямой равно длине отрезка, проведенного перпендикулярно из точки к этой прямой. ВМ⊥МЕ и является проекцией наклонной СМ. По т. о 3-х перпендикулярах СМ⊥МЕ и является искомым расстоянием. ВМ=8 см, СВ=6 см ⇒ ∆ ВСМ - египетский. СМ=10 см ( можно проверить по т.Пифагора).
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: lerabebe612
Предмет: История,
автор: lisi4kaolesa
Предмет: Литература,
автор: htrrtu0
Предмет: Физика,
автор: KonstantinovaCv
Предмет: Алгебра,
автор: Аноним