Предмет: Алгебра,
автор: Olga2021
представьте многочлен в виде куба суммы или куба разности двух выражений: а^3+6a^2b+12ab^2+8b^3. упростите выражения: u^3/8+3u^2v/2+6uv^2+8v^3. Возведите в степень: (a+2b)^3
Ответы
Автор ответа:
0
Формула куба суммы и разности:




Автор ответа:
0
Ответ ответ ответ ответ ответ ответ
Приложения:
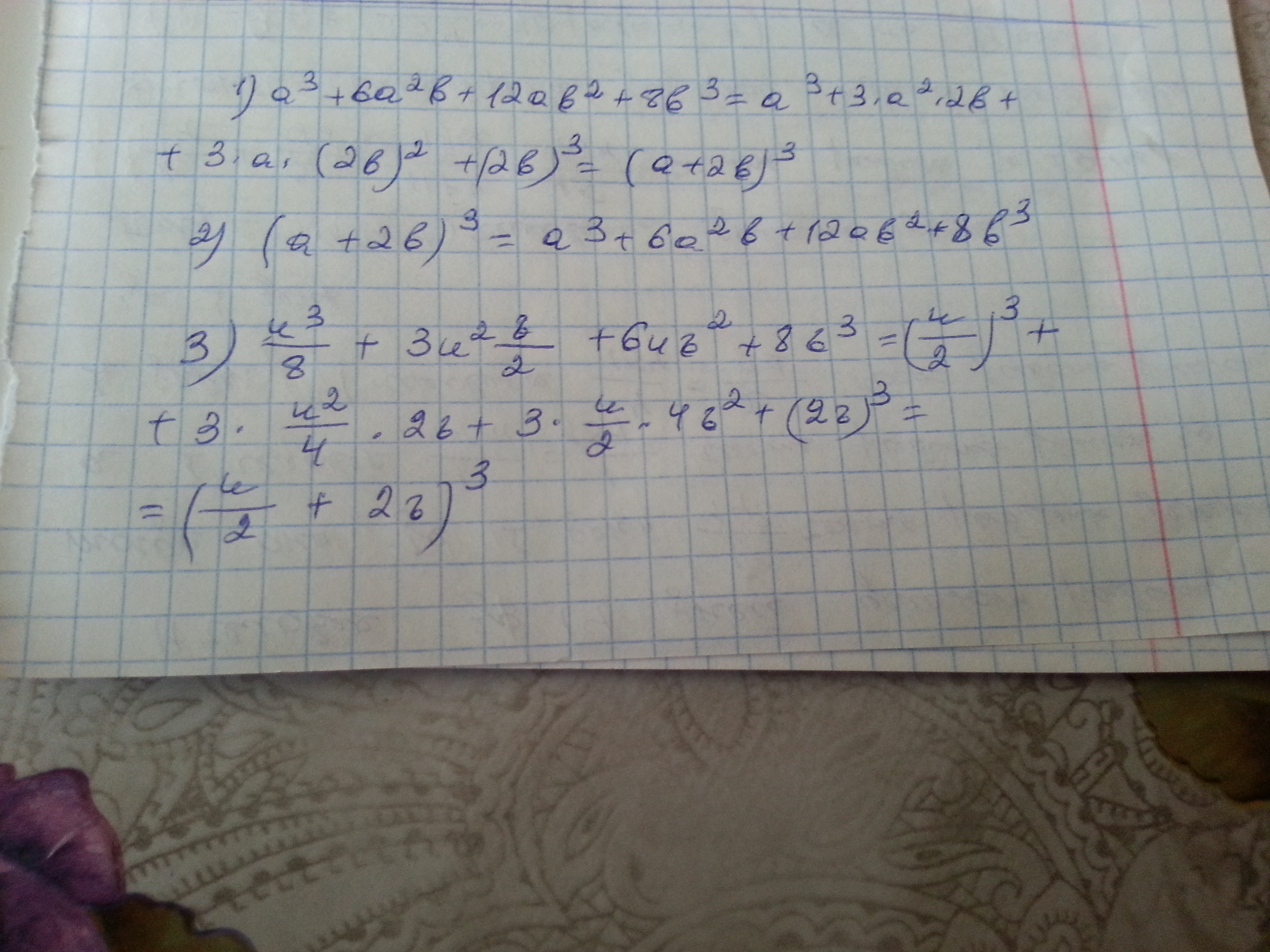
Похожие вопросы
Предмет: Английский язык,
автор: ilyadistream942
Предмет: Английский язык,
автор: 442388
Предмет: Обществознание,
автор: Аноним
Предмет: История,
автор: МихаилБелоножкин
Предмет: Математика,
автор: Vova578