Предмет: Математика,
автор: Locstar
Имеется 3 окружности, радиусы которых равны 3 ; 6 ; 9. Эти окружности касаются внешним образом. Найти радиус окружности, вписанной в треугольник, вершины которого являются центры этих 3-х окружностей
Пожалуйста, помогите мне(
Ответы
Автор ответа:
0
Радиус вписанной окружности равен:
r=S/p
r=√ ((p-a)(p-b)(p-c))/ p
p - полупериметр треугольника ОО₁О₂, в который вписана окружность
Найдем стороны треугольника ОО₁О₂. Они состоят из радиусов трех окружностей.
ОО1=3+6=9
О1О2=6+9=15
О2О=9+3=12
r=(9+15+12):2=18
r=√((18-9)(18-12)(18-15)) / 18
r=√18/18
r=1
Приложения:
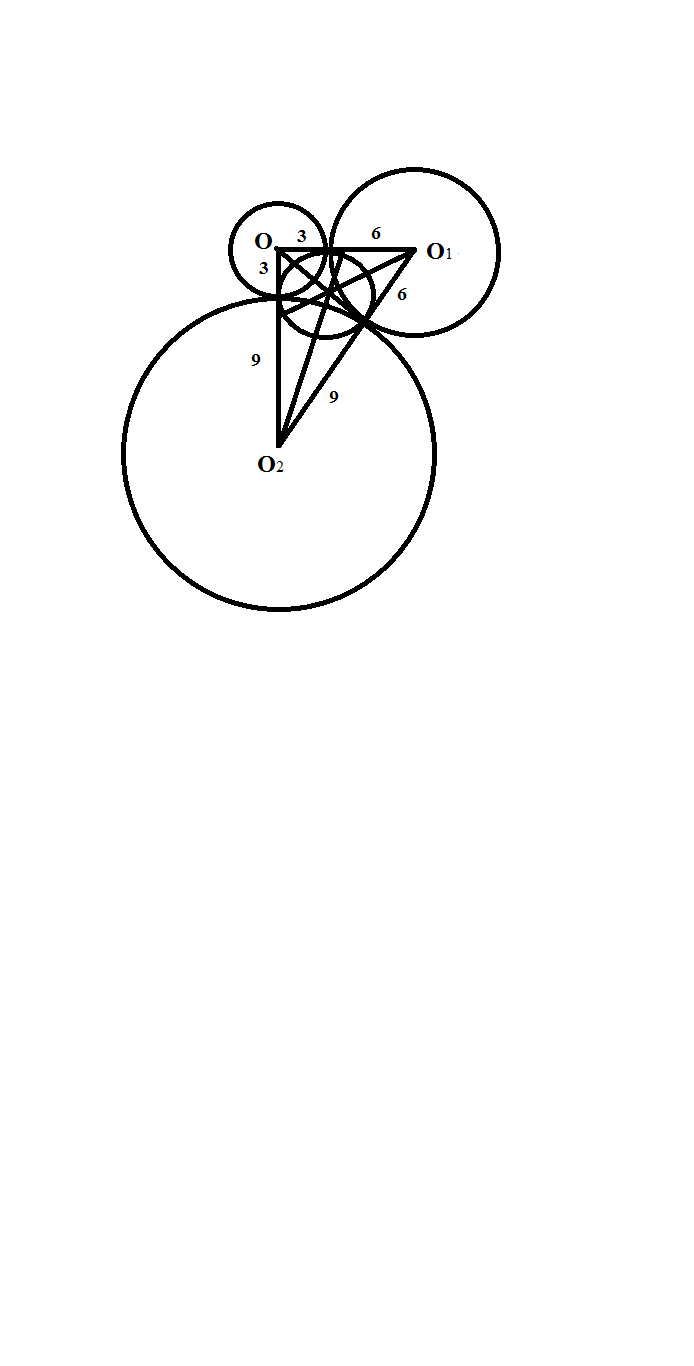
Автор ответа:
0
Радиус вписанной в треугольник окружности равен корню квадратному из дроби, в числителе которой - (р-а)(р-в)(р-с), а в знамнателе - р (полупериметр сторон треугольника), т.е. (а+в+с)/2= (15+12+9)/2= 18. Числитель равен (18-15)(18-12)(18-9)=3*6*9. Итак, искомый радиус = корню квадратному из 3*6*9/18 = 3.!!!
Чертеж не прилагаю, т.к. он очевиден.
Приложения:
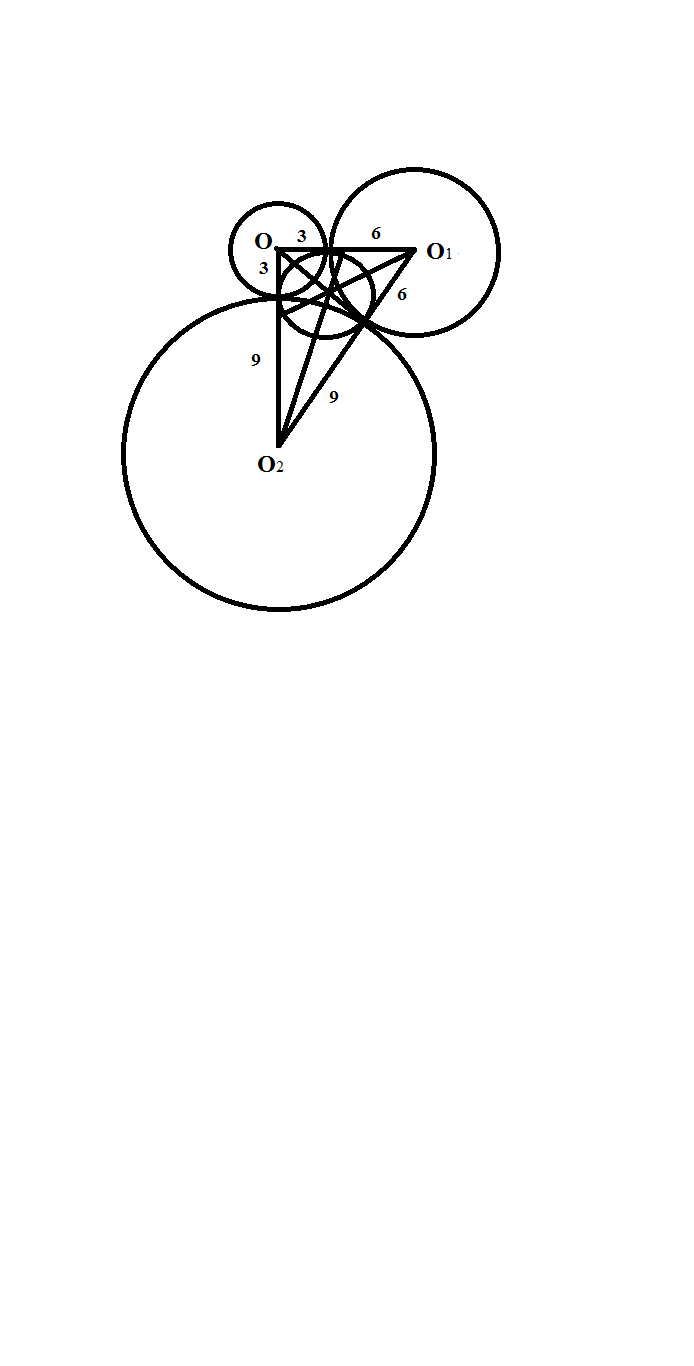
Похожие вопросы
Предмет: Физика,
автор: mukashovs83
Предмет: Алгебра,
автор: aovcinnikov108
Предмет: Русский язык,
автор: akmaraltleubaeva417
Предмет: Физика,
автор: Glazkova
Предмет: Математика,
автор: nifirtiti37