Предмет: Алгебра,
автор: galkaaz
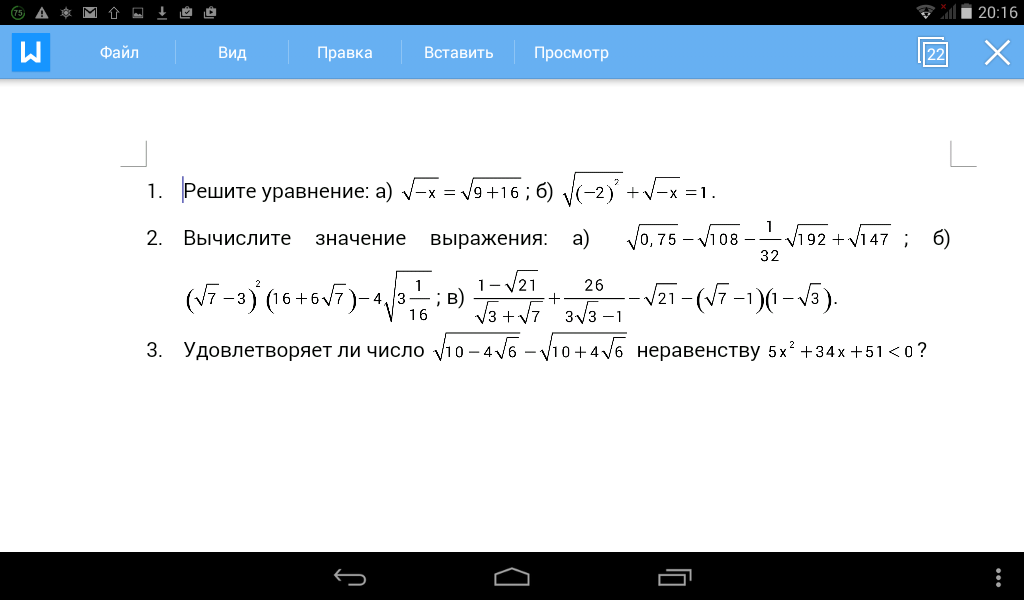
Решите пожалуйста второй и третий номер.
Приложения:
Ответы
Автор ответа:
0
Число х=-4 удовлетворяет заданному неравенству.
Похожие вопросы
Предмет: Математика,
автор: sabieva2702
Предмет: Русский язык,
автор: aruzhanmubarakova07
Предмет: Английский язык,
автор: chdfffdggg
Предмет: Математика,
автор: Валерочка500
Предмет: Геометрия,
автор: FLESHPIT1