Предмет: Алгебра,
автор: fantasticgirl
Решите логарифмическое уравнение! Буду очень признательна. Плоховасто видно, поэтому запишу таким образом:
log^2 0.5(x-5)+log 2(4/x-5)=(3/5)^log 3/5 1/4+ log 3/5 8
Приложения:
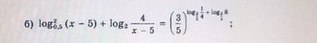
Ответы
Автор ответа:
0
ОДЗ:
x-5>0
x>5
1)
2)
2 способ:
1)
2)
Ответ: 6; 7.
Автор ответа:
0
А если приводить к основанию 2, а не 1/2? Получится такой же ответ?
Автор ответа:
0
да
Автор ответа:
0
У меня почему-то не сходится. Посмотрите, пожалуйста
2. log2(x-5)=-1
log2(x-5)=log2(1/2)
x-5=1/2
2. log2(x-5)=-1
log2(x-5)=log2(1/2)
x-5=1/2
Автор ответа:
0
В самом решении написан второй способ при основании 2.
Автор ответа:
0
Большое спасибо )
Похожие вопросы
Предмет: Экономика,
автор: mahmudovanigora318
Предмет: Математика,
автор: lerakovalenko2020
Предмет: Геометрия,
автор: mihelalexandr03
Предмет: Математика,
автор: тоха1242
Предмет: География,
автор: rmraka