Предмет: Геометрия,
автор: Agent007Pro
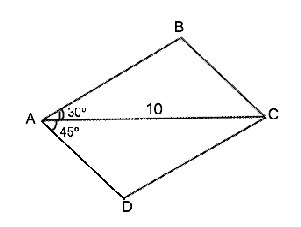
В параллелограмме ABCD диагональ AC=10. Найти площадь параллелограмма ABCD, если угол BAC=30°, угол DAC=45°.
Приложения:
Ответы
Автор ответа:
0
Угол ВАD=∠BAC+∠CAD=75°. ВС|║AD, АВ- секущая. Сумма внутренних углов при пересечении параллельных прямых секущей равна 180°. ⇒ ∠ВАD=180°-75°=105°. В ∆ АВС ∠ВСА=∠САD=45°- накрестлежащие. Из ∆ АВС по т. синусов АС:sin105°=AB:sin45°. Синус 105°=sin75°=(√3+1):2√2.
10:((√3+1)/2√2)=AB:((√2):2), откуда АВ=20:(√3+1)
Ѕ(АВС)=0,5•АВ•АС•sin(BAC)=[10•20:(√3+1)]:4=50:(√3+1)
∆ АDC=∆АВС=> S(ABCD)=2•50:(√3+1)=36,6025…≈36,6
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kira45392
Предмет: Английский язык,
автор: isenovdaniar254
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: Svetlana2222gg
Предмет: Математика,
автор: vkostyuk11