Предмет: Алгебра,
автор: Ksi0210
Помогите найти производную
Приложения:
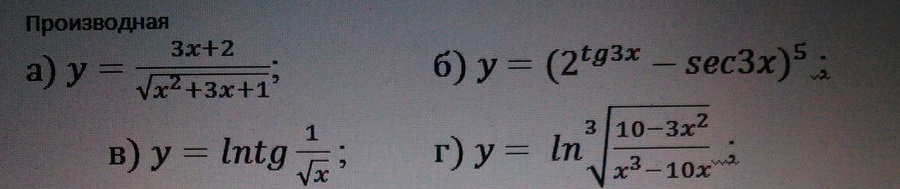
Ответы
Автор ответа:
0
a)


б)

в)


г)
![y=ln sqrt[3]{ frac{10-3x^2}{x^3-10x} } \
\
y'= frac{1}{ sqrt[3]{ frac{10-3x^2}{x^3-10x} } }* frac{1}{3}*( frac{10-3x^2}{x^3-10x} )^{- frac{2}{3} }*( frac{-6x(x^3-10x)-(10-3x^2)(3x^2-10)}{(x^3-10x)^2} )= y=ln sqrt[3]{ frac{10-3x^2}{x^3-10x} } \
\
y'= frac{1}{ sqrt[3]{ frac{10-3x^2}{x^3-10x} } }* frac{1}{3}*( frac{10-3x^2}{x^3-10x} )^{- frac{2}{3} }*( frac{-6x(x^3-10x)-(10-3x^2)(3x^2-10)}{(x^3-10x)^2} )=](https://tex.z-dn.net/?f=y%3Dln+sqrt%5B3%5D%7B+frac%7B10-3x%5E2%7D%7Bx%5E3-10x%7D+%7D+%5C+%0A+%5C+%0Ay%27%3D+frac%7B1%7D%7B+sqrt%5B3%5D%7B+frac%7B10-3x%5E2%7D%7Bx%5E3-10x%7D+%7D+%7D%2A+frac%7B1%7D%7B3%7D%2A%28+frac%7B10-3x%5E2%7D%7Bx%5E3-10x%7D+%29%5E%7B-+frac%7B2%7D%7B3%7D+%7D%2A%28+frac%7B-6x%28x%5E3-10x%29-%2810-3x%5E2%29%283x%5E2-10%29%7D%7B%28x%5E3-10x%29%5E2%7D+%29%3D+++)


б)
в)
г)
Похожие вопросы
Предмет: Геометрия,
автор: erikkurwa
Предмет: История,
автор: grunovivan10
Предмет: Математика,
автор: max5521
Предмет: Математика,
автор: мариша1984
Предмет: Математика,
автор: фатя2002