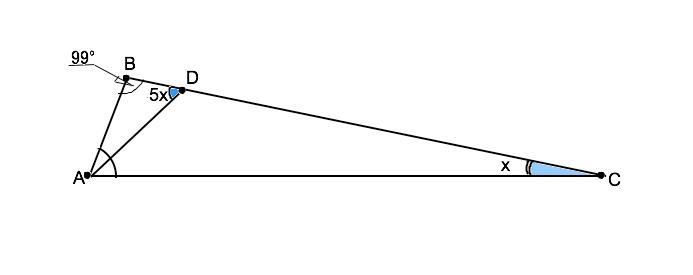
В треугольнике ABC угол В равен 99 градусов,AD-биссектриса угла А,угол С меньше угла ADB в пять раз.Найдите градусную меру угла С.
Ответы
Пусть угол С=х градусов.
Рассмотрим два треугольника, которые после проведения биссектрисы образовались из треугольника АВС.
В треугольнике АВD
угол В=99°,
угол D=5хугол А=180° -(99°+5х)
В треугольнике АDС
Угол С=х
Угол АDС=180°-х
Угол А=180°-(180°-5х+х)
Приравняем два значения угла А:
180° -(99°+5х)=180°-(180°-5х+х)
180 - 99 - 5х =180 - 180 + 5х -х
81°=9х
х=9°
Ответ: угол С=9°.
Вариант решения: Примем угол С равным х. Тогда угол ADB=5x. По свойству внешнего угла для ∆ АDC он равен сумме внутренних, не смежных с ним. ∠АDB= ∠DAC+∠DCA = 5х ⇒ угол DAC=5х-х=4х. АD – биссектриса, поэтому ∠ВАС=2∠DAC=8х. Из суммы углов треугольника ∠А+∠В+∠С=180°⇒
8х+99°+х=180° ⇒ ∠С=х=81:9=9°
Проверка:
угол А=180-99-9=72°
Из треугольника АDС
Угол А:2=180- 9-(180-45)=36°
72:2=36°