Предмет: Алгебра,
автор: nastasiya95
отдам 50 баллов за ПРАВИЛЬНОЕ решение
Приложения:
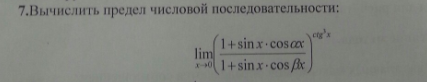
Ответы
Автор ответа:
0
Этот предел с неопределенностью типа  . Его можно вычислить, приведя ко второму замечательному пределу. Можно также использовать логарифмирование, правило Лопиталя и первый замечательный предел. Это и было сделано ниже.
. Его можно вычислить, приведя ко второму замечательному пределу. Можно также использовать логарифмирование, правило Лопиталя и первый замечательный предел. Это и было сделано ниже.



Похожие вопросы
Предмет: Русский язык,
автор: esorokolet9
Предмет: Қазақ тiлi,
автор: ramazan15izturganov
Предмет: Алгебра,
автор: lolotrek227
Предмет: Математика,
автор: Elizavetoshka1