Предмет: Математика,
автор: kiyashko91
Обратная матрица. Найти обратную матрицу к матрице А и проверить выполнение равенства. n =4 m =1
Приложения:
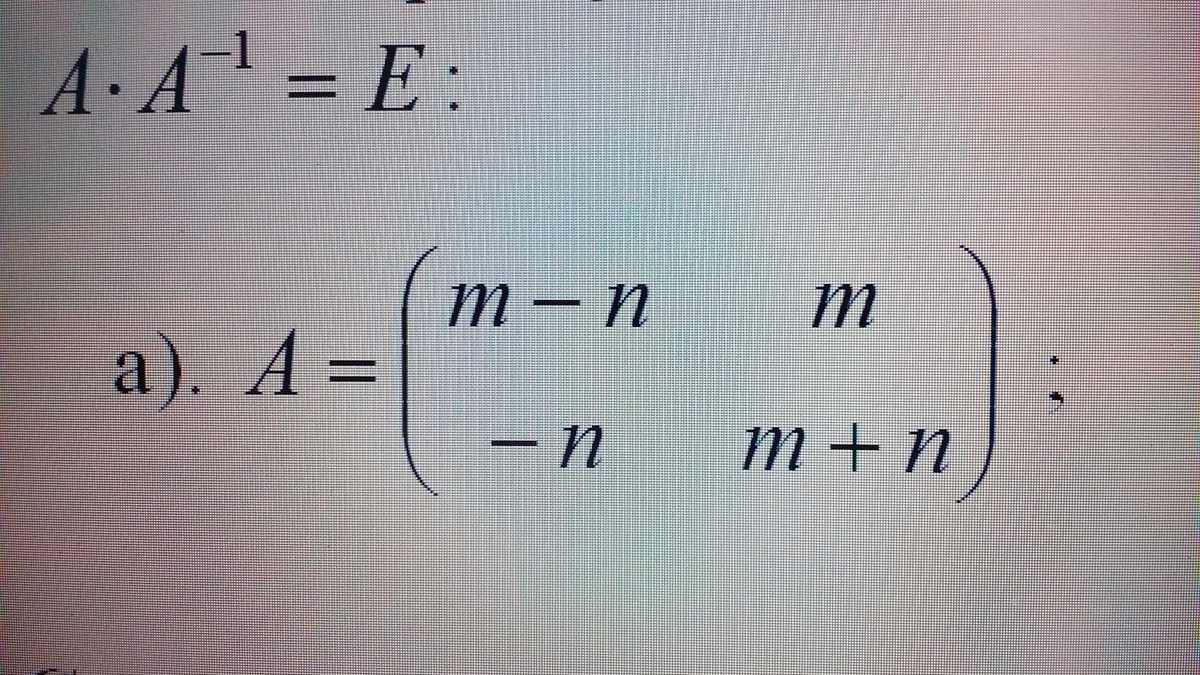
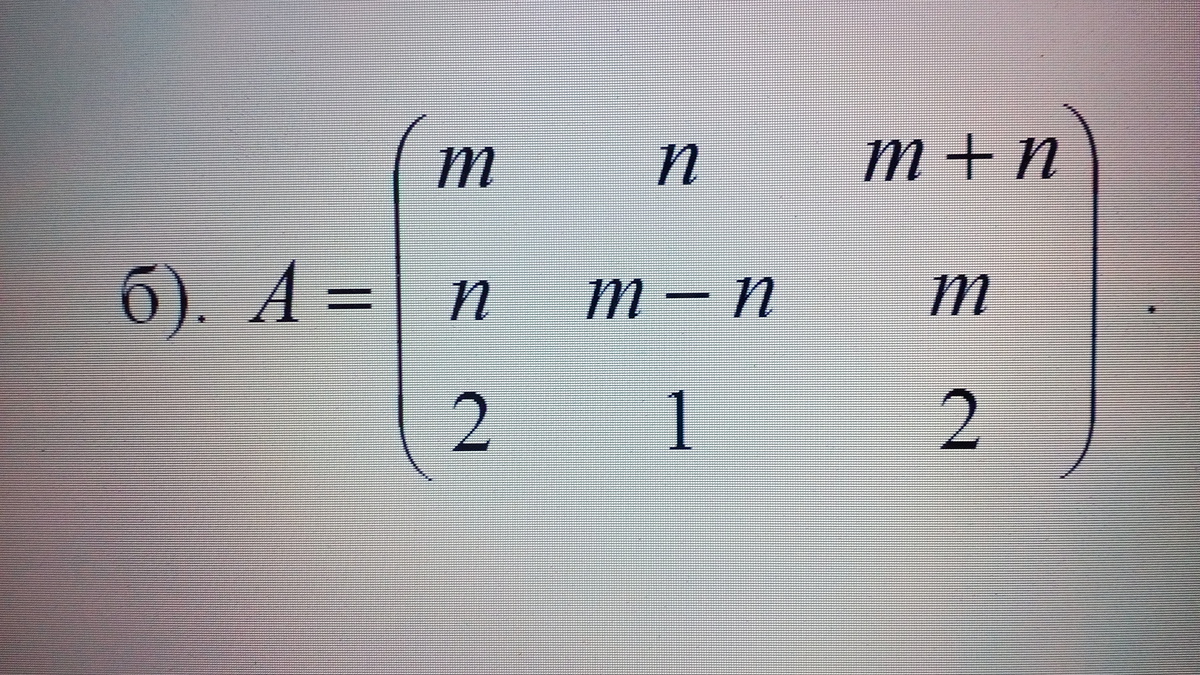
Ответы
Автор ответа:
0
Подставляем
Проверять даже смысла нет . Т.к
б) A =
Методом Гаусса ищем обратную
Похожие вопросы
Предмет: Қазақ тiлi,
автор: faridaubekerov
Предмет: Қазақ тiлi,
автор: ie4rt
Предмет: Қазақ тiлi,
автор: irhinnikita214
Предмет: Физика,
автор: vasyaglotov