Предмет: Геометрия,
автор: manaka1294
В треугольнике ABC известно, что AB=BC=50, AC=96. Найдите длину медианы BM. Прошу помогите
Ответы
Автор ответа:
0
Решение:
1.ΔАВС - равнобедренный(так как АВ=ВС(ПО УСЛОВИЮ))
2. ВМ - медиана по условию,значит и высота (так как в равнобедренном треугольнике медиана является и биссектрисой, и высотой)
3.∠АМВ=90°(так как МВ - высота)
4. АС=АМ+МС; АМ=МС (та как МВ - медиана), значит АМ=АС/2=96°/2=48°
5.ΔАМВ - прямоугольный, значит по теореме Пифагора:
ВМ²+АМ²=АВ²
ВМ²+48²=50²
ВМ=√(50²-48²)=14
Ответ:14
1.ΔАВС - равнобедренный(так как АВ=ВС(ПО УСЛОВИЮ))
2. ВМ - медиана по условию,значит и высота (так как в равнобедренном треугольнике медиана является и биссектрисой, и высотой)
3.∠АМВ=90°(так как МВ - высота)
4. АС=АМ+МС; АМ=МС (та как МВ - медиана), значит АМ=АС/2=96°/2=48°
5.ΔАМВ - прямоугольный, значит по теореме Пифагора:
ВМ²+АМ²=АВ²
ВМ²+48²=50²
ВМ=√(50²-48²)=14
Ответ:14
Приложения:
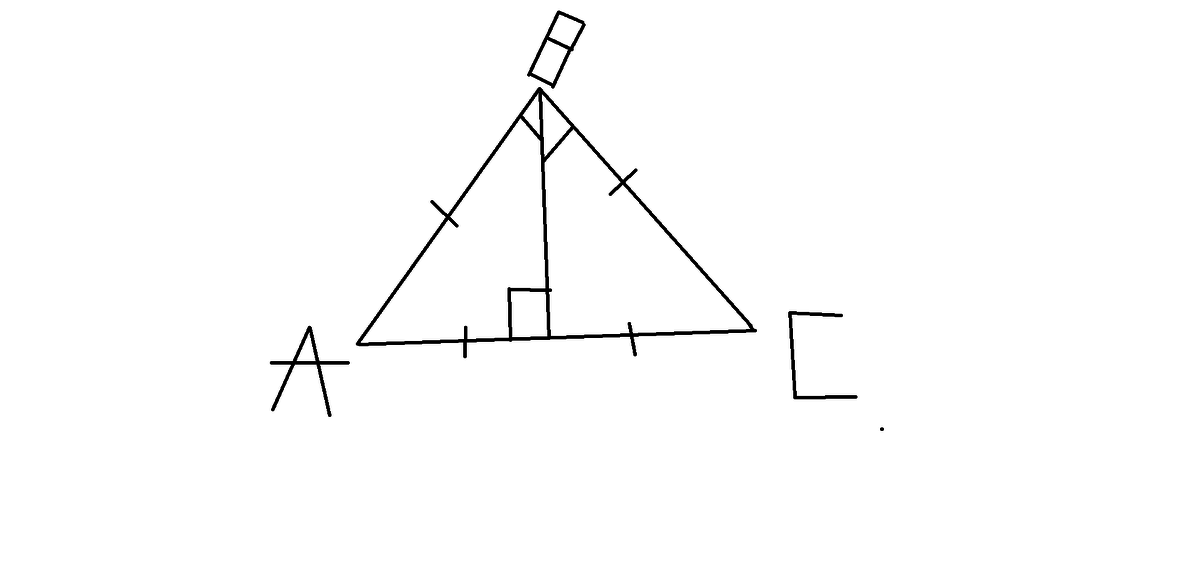
Похожие вопросы
Предмет: Русский язык,
автор: maryagusak
Предмет: Беларуская мова,
автор: ulanaakimec401
Предмет: Математика,
автор: galinabuglova04203
Предмет: Обществознание,
автор: nastyamaltseva