Question

постройте график функции у 6х+7/6х^2+7х и определите, при каких значениях прямая у=кх имеет с графиком ровно одну общую точку. ^ -ЭТО ЗНАЧИТ СТЕПЕНЬ! В квадрате только 6х

Answer 1

Область определения функции:

$6x^2+7xne 0\ x(6x+7)ne 0\ x_1ne 0\ x_2ne-frac{7}{6}$

Упростим функцию $y=dfrac{6x+7}{6x^2+7x}=dfrac{6x+7}{x(6x+7)}=dfrac{1}{x}$

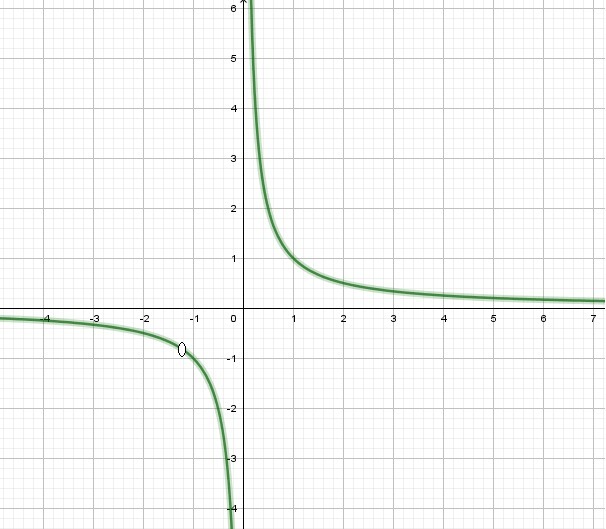
Получили гиперболу. Подставив х=-7/6, получим у=-6/7. То есть, точка (-7/6;-6/7) - выколотая точка

Подставим y=kx в упрощенную функцию, имеем kx=1/x

kx² = 1

x² = 1/k

При k≤0 уравнение решений не имеет, при k>0 уравнение имеет два действительных корня.

Теперь подставим точку (-7/6;-6/7) в функцию y=kx, получим

$-frac{6}{7} =kcdot(-frac{7}{6})\ \ k=frac{36}{49}$

При k=36/49 графики пересекаются в одной точке.