Предмет: Математика,
автор: Lily961
Вычислить площадь (плоской) фигуры, ограниченной линиями:
(во вложений)
С полным решением. Помогите пожалуйста...
Приложения:
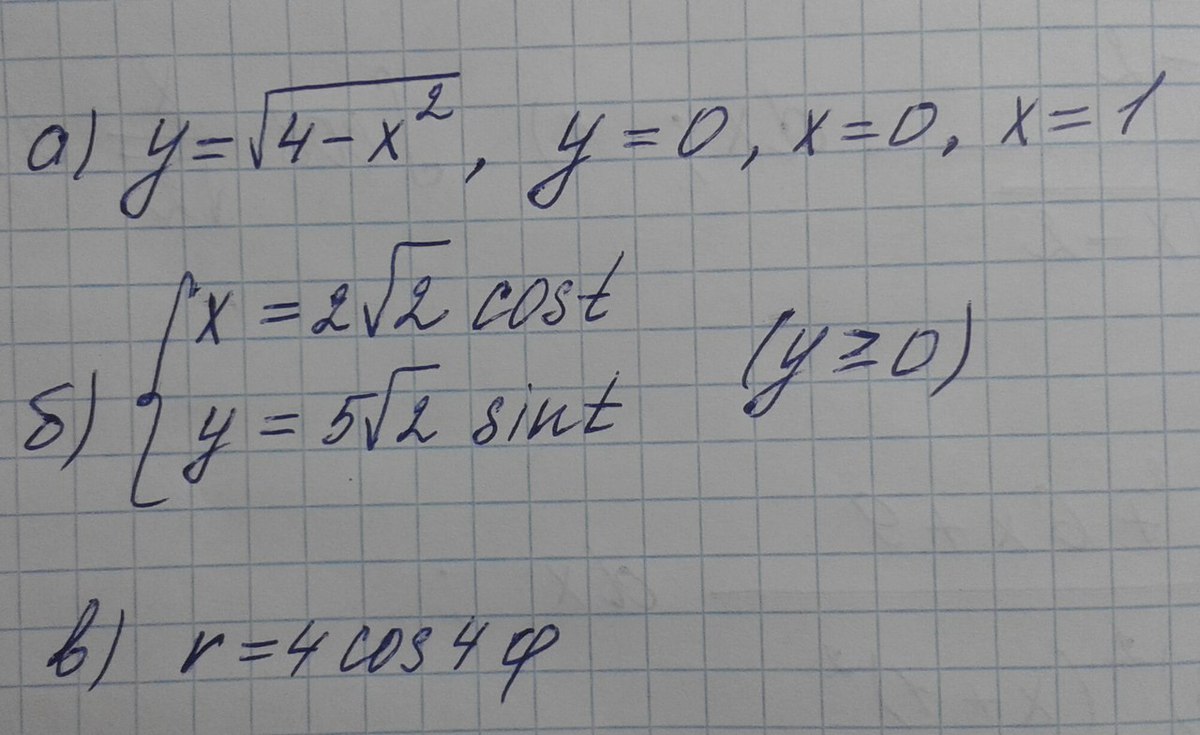
Ответы
Автор ответа:
0
Вычислить площадь плоской фигуры ограниченной линиями
 , y=0, x=0, x=1
, y=0, x=0, x=1
Решение:
Графики линий и сама плоская фигура начерчены в файлах.
Площадь фигуры найдем по формуле

Найдем в начале неопределенный интеграл применим подстановку новой переменной х=2sin(u)





Производим обратную замену sin(u)=x/2, u=arcsin(x/2)


Поэтому неопределенный интеграл равен

Находим площадь фигуры



Ответ: S=π/3+√3/2≈1,913
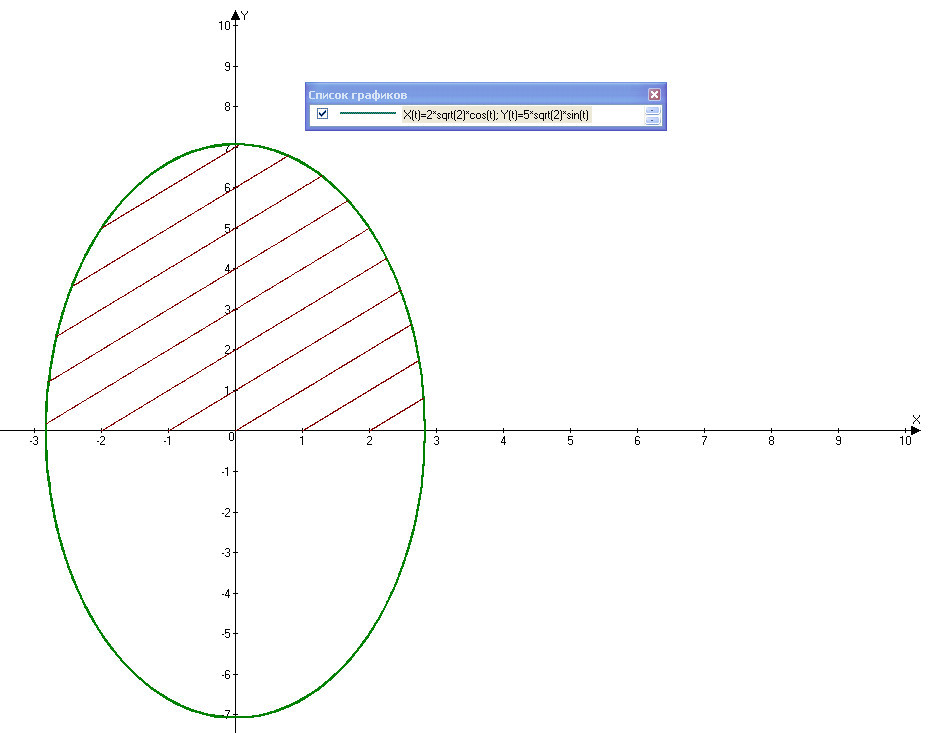
б)
Графики линий и сама плоская фигура начерчены в файлах.
Площадь фигуры найдем по формуле

Производная переменной х по t равна




Ответ: 10π≈31,4
в) r =4сos( )
)
Плоская фигура начерчена в файлах.
Площадь фигуры найдем по формуле

Так как фигура состоит из 8 одинаковых симметричных лепестков, то определим площадь половинки лепестка и умножим на 16. При этом углы интегрирования будут равны





Решение:
Графики линий и сама плоская фигура начерчены в файлах.
Площадь фигуры найдем по формуле
Найдем в начале неопределенный интеграл применим подстановку новой переменной х=2sin(u)
Производим обратную замену sin(u)=x/2, u=arcsin(x/2)
Поэтому неопределенный интеграл равен
Находим площадь фигуры
Ответ: S=π/3+√3/2≈1,913
б)
Графики линий и сама плоская фигура начерчены в файлах.
Площадь фигуры найдем по формуле
Производная переменной х по t равна
Ответ: 10π≈31,4
в) r =4сos(
Плоская фигура начерчена в файлах.
Площадь фигуры найдем по формуле
Так как фигура состоит из 8 одинаковых симметричных лепестков, то определим площадь половинки лепестка и умножим на 16. При этом углы интегрирования будут равны
Приложения:


Автор ответа:
0
В файлах начерчены плоские фигуры
Похожие вопросы
Предмет: Русский язык,
автор: askatovaaiperi98
Предмет: Русский язык,
автор: tomiris07777
Предмет: Английский язык,
автор: Аноним
Предмет: География,
автор: hekenebelle5
Предмет: Математика,
автор: 12345321