Предмет: Математика,
автор: fikus2
Помогите 66 пожалуйста!Буду вам очень благодарна
Приложения:
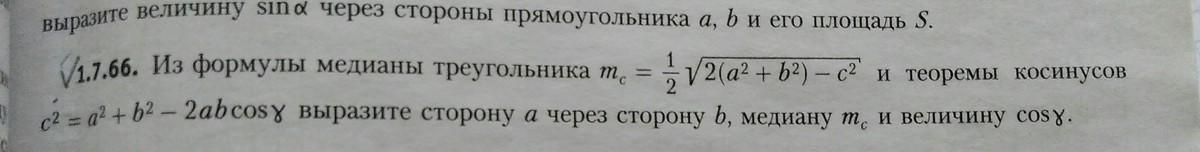
Ответы
Автор ответа:
0
Возведём в квадрат выражение для медианы  , проведённой к стороне
, проведённой к стороне  предварительно умножив его на
предварительно умножив его на  , и получим:
, и получим:
 ;
;
Используя теорему косинусов для исключения значения из искомого выражения, получим:
из искомого выражения, получим:
 ;
;
 ;
;
 ;
;
![a^2 + [ 2b cos{ gamma } ] cdot a - [ ( 2 m_c )^2 - b^2 ] = 0 a^2 + [ 2b cos{ gamma } ] cdot a - [ ( 2 m_c )^2 - b^2 ] = 0](https://tex.z-dn.net/?f=+a%5E2+%2B+%5B+2b+cos%7B+gamma+%7D+%5D+cdot+a+-+%5B+%28+2+m_c+%29%5E2+-+b%5E2+%5D+%3D+0+) ;
;
Итак, мы получили параметрическое приведённое квадратное уравнение (старший коэффициент равен единице) с чётным центральным линейным коэффициентом где
где  и свободным слагаемым
и свободным слагаемым ![p = - [ ( 2 m_c )^2 - b^2 ] p = - [ ( 2 m_c )^2 - b^2 ]](https://tex.z-dn.net/?f=+p+%3D+-+%5B+%28+2+m_c+%29%5E2+-+b%5E2+%5D+) ;
;
Его решения выражаются, как:
 где
где 
где чётно-приведённый дискриминант выражается, как:
выражается, как:

и: ;
;
В итоге:
 ;
;
На первый взгляд, может обманчиво (!) показаться, что при использовании перед корнем из дискриминанта знака «минус», решение в целом будет отрицательным, а стало быть, нужно брать только одно решение со знаком «плюс» перед корнем из дискриминанта. НО ЭТО НЕ ТАК! Если угол – тупой, то
– тупой, то  и слагаемое
и слагаемое ![[ -cos{ gamma } ] > 0 [ -cos{ gamma } ] > 0](https://tex.z-dn.net/?f=+%5B+-cos%7B+gamma+%7D+%5D+%26gt%3B+0+) , так что если это слагаемое по модулю будет больше корня из дискриминанта, то оба решения будут положительными и значит при заданных медиане
, так что если это слагаемое по модулю будет больше корня из дискриминанта, то оба решения будут положительными и значит при заданных медиане  стороне
стороне  и значения угла
и значения угла  – будут возможны два варианта стороны
– будут возможны два варианта стороны  и соответственно два несколько различных треугольника!
и соответственно два несколько различных треугольника!
Чтобы понять, когда второй корень будет тоже положительным, потребуем:
 ;
;
 ;
;
 при
при  ;
;
 ;
;
 ;
;
 ;
;
 поскольку:
поскольку:  и
и  то:
то:
 ;
;
 ;
;
 – именно при таком условии, в случае, когда угол
– именно при таком условии, в случае, когда угол  – тупой, имеется два различных решения для
– тупой, имеется два различных решения для  и два различных треугольника.
и два различных треугольника.
О т в е т :
Если угол – тупой, и медиана
– тупой, и медиана  то существует два различных треугольника со сторонами:
то существует два различных треугольника со сторонами:
 ;
;
Иначе, если угол – острый или прямой, или если медиана
– острый или прямой, или если медиана  то решение единственно:
то решение единственно:

Используя теорему косинусов для исключения значения
Итак, мы получили параметрическое приведённое квадратное уравнение (старший коэффициент равен единице) с чётным центральным линейным коэффициентом
Его решения выражаются, как:
где чётно-приведённый дискриминант
и:
В итоге:
На первый взгляд, может обманчиво (!) показаться, что при использовании перед корнем из дискриминанта знака «минус», решение в целом будет отрицательным, а стало быть, нужно брать только одно решение со знаком «плюс» перед корнем из дискриминанта. НО ЭТО НЕ ТАК! Если угол
Чтобы понять, когда второй корень будет тоже положительным, потребуем:
О т в е т :
Если угол
Иначе, если угол
Автор ответа:
0
Успехов вам!
Автор ответа:
0
Согласно действующим (!) правилам русской орфографии и пунктуации 1956 года «с прописной буквы пишутся индивидуальные названия, относящиеся к области религии и мифологии, например: Христос, Будда, Зевс, Венера, Вотан, Перун, Молох... Индивидуальные названия мифологических существ, превратившиеся в имена нарицательные, пишутся со строчной буквы, например: молох коммунизма».
Автор ответа:
0
По правилам: слово «бог» пишется со строчной буквы, в том числе по отношению к единому божеству и при воспроизведении дореволюционных текстов. В справочнике Правила русской орфографии и пунктуации РАН (2007) «С прописной буквы рекомендуется (! но не требуется) писать слово «Бог» как название единого верховного существа (в монотеистических религиях),
Автор ответа:
0
а слово «бог» в формах множественного числа, а также в значении одного из множества «богов» или в переносном значении пишется со строчной буквы, например: боги Олимпа, бог Аполлон, бог войны и т.п.». В поговорках и междометиях слово пишется со строчной буквы: ей-богу, бог знает кто, о господи и т.п.
Автор ответа:
0
Удачи вам!
Похожие вопросы
Предмет: Русский язык,
автор: alecsandramertins
Предмет: Қазақ тiлi,
автор: daria999nd
Предмет: Алгебра,
автор: Аноним
Предмет: Литература,
автор: Аноним