Предмет: Геометрия,
автор: 19071976
Биссектриса внешнего угла при вершине A треугольника ABC параллельна его стороне
BC. Верно ли, что треугольник ABC равнобедренный?
Ответы
Автор ответа:
0
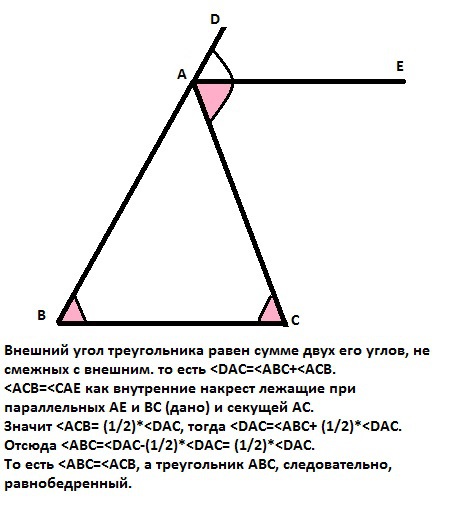
Внешний угол треугольника равен сумме двух его углов, не смежных с внешним. то есть <DАC=<АВC+<AСВ.
<AСВ=<CАE как внутренние накрест лежащие при параллельных АЕ и ВС (дано) и секущей АС.
Значит <АСВ= (1/2)*<DАC, тогда <DАC=<АВС+(1/2)*<DАC.
Отсюда <АВС=<DАC-(1/2)*<DАC= (1/2)*<DАC.
То есть <АВС=<АСВ, а треугольник АВС, следовательно, равнобедренный.
<AСВ=<CАE как внутренние накрест лежащие при параллельных АЕ и ВС (дано) и секущей АС.
Значит <АСВ= (1/2)*<DАC, тогда <DАC=<АВС+(1/2)*<DАC.
Отсюда <АВС=<DАC-(1/2)*<DАC= (1/2)*<DАC.
То есть <АВС=<АСВ, а треугольник АВС, следовательно, равнобедренный.
Приложения:
Автор ответа:
0
Решение будет то же самое, только буквы переставлю.
Автор ответа:
0
будьте добры,переставьте
Автор ответа:
0
Не правильно
Автор ответа:
0
Согласен. А исправить?
Автор ответа:
0
Хотя не вижу ошибки. Можно и так (что то же самое) : Или так: <DAE=<BCA как соответственные при параллельных АЕ и ВС и секущей DC. <ABC=<BAE как внутренние накрест лежащие при параллельных АЕ и ВС и секущей АВ. Но <DAE=<BAE (АЕ - биссектриса). Значит <B=<C.
Похожие вопросы
Предмет: Математика,
автор: kasymovarysolat52
Предмет: Русский язык,
автор: Аноним
Предмет: География,
автор: Аноним
Предмет: Математика,
автор: tahfgk
Предмет: Математика,
автор: aidana2014kg