Question

высота ромба равна 2√6 ,а косинус угла между его высотой и меньшей диагональю рааен 0,6.Найдите площадь ромба

Answer 1

Ответ:

Sabcd = 25 ед².

Пошаговое объяснение:

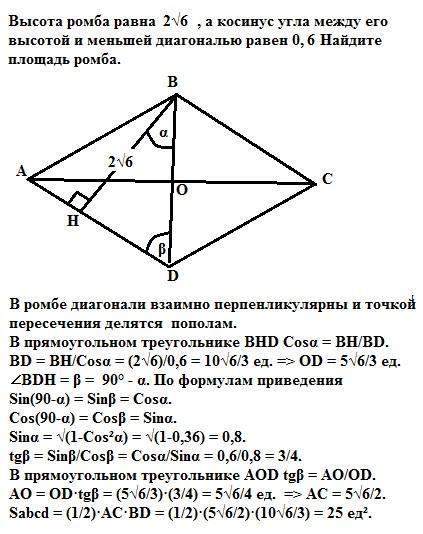
В ромбе диагонали взаимно перпенликулярны и точкой пересечения делятся пополам.

В прямоугольном треугольнике ВНD Cosα = BH/BD.

BD = BH/Cosα = (2√6)/0,6 = 10√6/3 ед. => ОD = 5√6/3 ед.

∠BDH = β =  90° - α. По формулам приведения

Sin(90-α) = Sinβ = Cosα.

Cos(90-α) = Cosβ = Sinα.  

Sinα = √(1-Cos²α) = √(1-0,36) = 0,8.

tgβ = Sinβ/Cosβ = Cosα/Sinα = 0,6/0,8 = 3/4.

В прямоугольном треугольнике AOD tgβ = AO/OD.

AO = OD·tgβ = (5√6/3)·(3/4) = 5√6/4 ед.  => AC = 5√6/2.

Sabcd = (1/2)·AC·BD = (1/2)·(5√6/2)·(10√6/3) = 25 ед².