Предмет: Алгебра,
автор: 2329095
Ребят , примерчики решите срочно!!! буду признательна
Приложения:
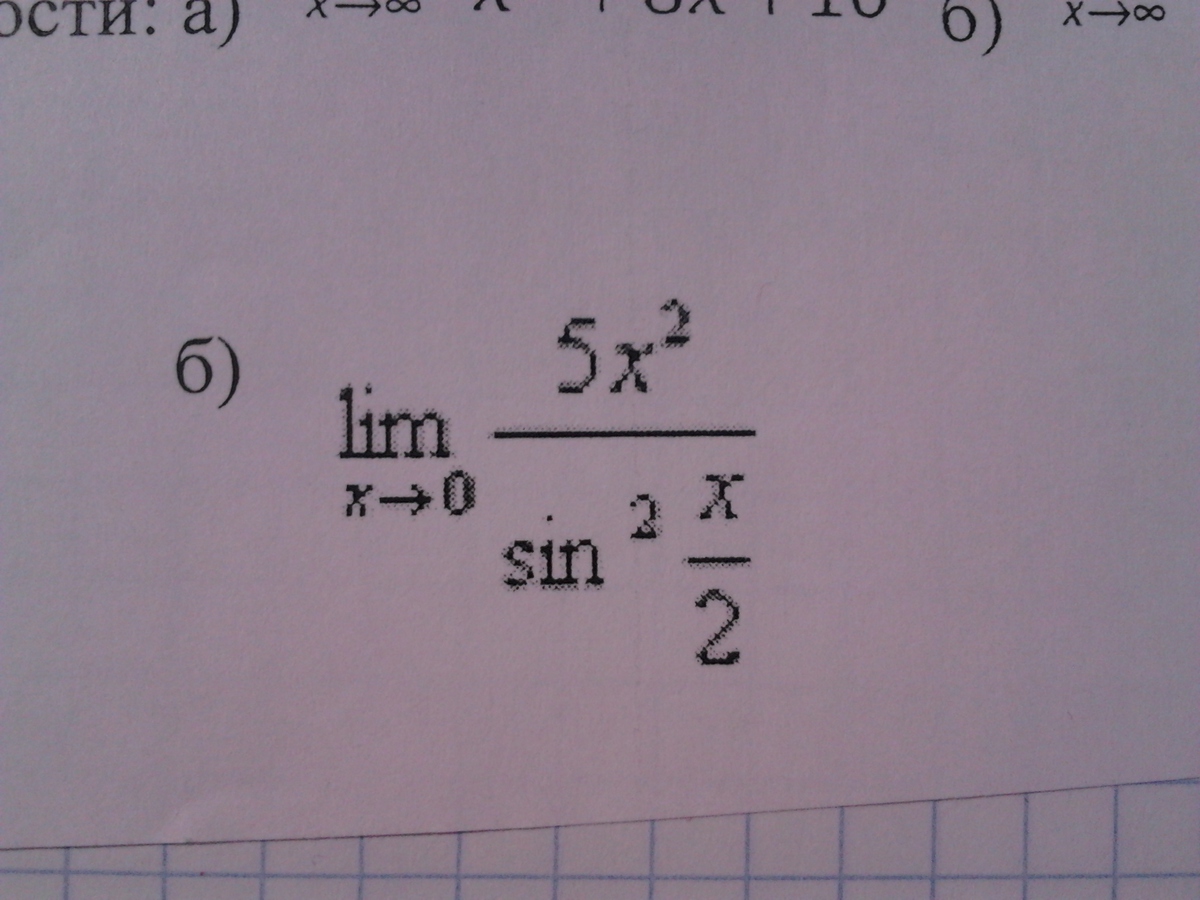
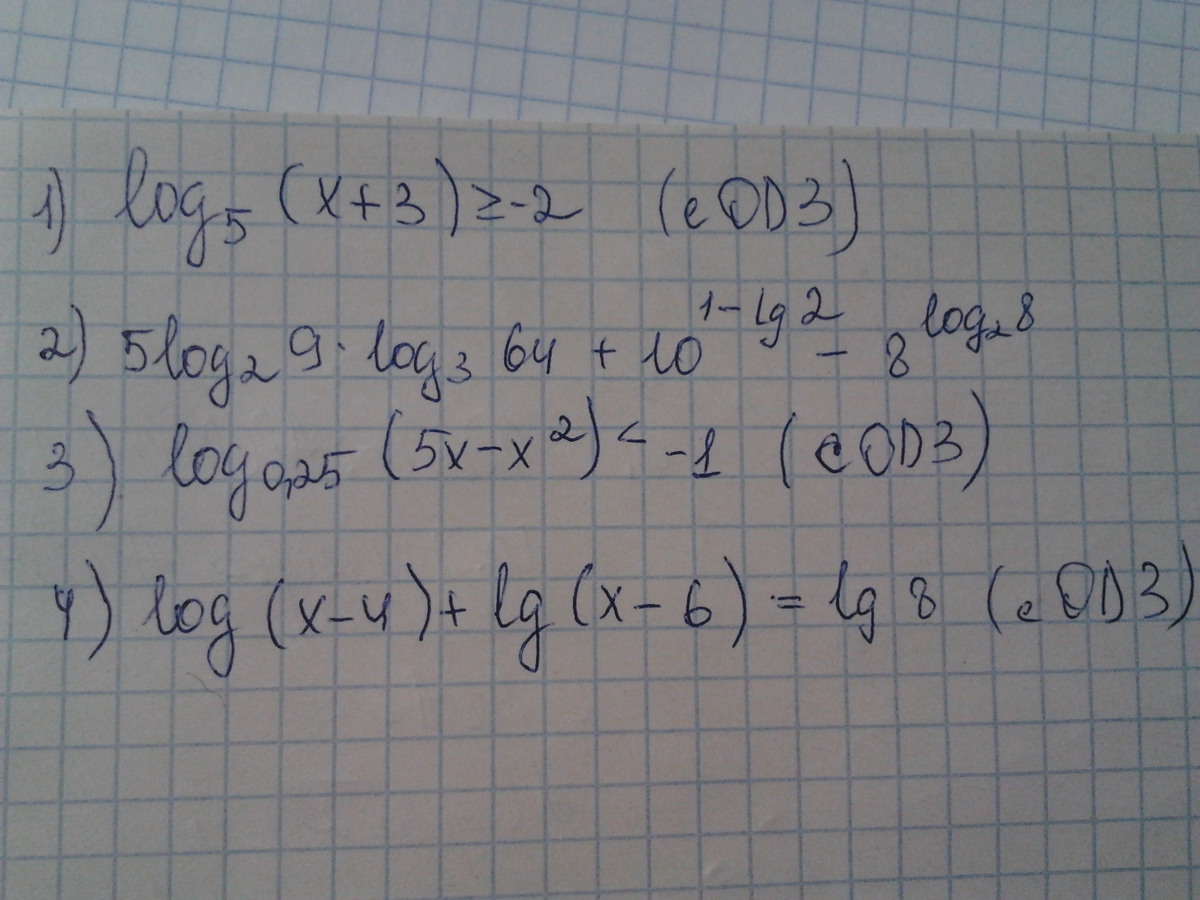
Ответы
Автор ответа:
0
1)

Ответ: x є [-2(24/25);+00)
2)


3)5x-x^2≤4 ОДЗ 5x-x^2>0 => x(5-x)>0 ; x>0 ; 5-x>0
-x^2+5x-4≤0
x^2-5x+4≥0
D=25-4*4=9
x1=4
x2=1
Берём -100. (-100)^2+500-4>0 То есть наш интервал имеет вид (-00;1]U[4;+00)
Т.к. одз x>0 ; x<5 тогда ответ X Є (0;1] U [4;5)
4)

x2=2 не принадлежит ОДЗ
Ответ: x є [-2(24/25);+00)
2)
3)5x-x^2≤4 ОДЗ 5x-x^2>0 => x(5-x)>0 ; x>0 ; 5-x>0
-x^2+5x-4≤0
x^2-5x+4≥0
D=25-4*4=9
x1=4
x2=1
Берём -100. (-100)^2+500-4>0 То есть наш интервал имеет вид (-00;1]U[4;+00)
Т.к. одз x>0 ; x<5 тогда ответ X Є (0;1] U [4;5)
4)
x2=2 не принадлежит ОДЗ
Автор ответа:
0
dc`
Автор ответа:
0
всё
Автор ответа:
0
В третьем ошибка біла
Автор ответа:
0
была, исправил
Автор ответа:
0
огромное вам спасибо !!!
Похожие вопросы
Предмет: Математика,
автор: konkaley1981
Предмет: Математика,
автор: myrsabekovuluk
Предмет: Геометрия,
автор: vdemutskagmailcom
Предмет: Математика,
автор: flalfa