Предмет: Алгебра,
автор: LordByron
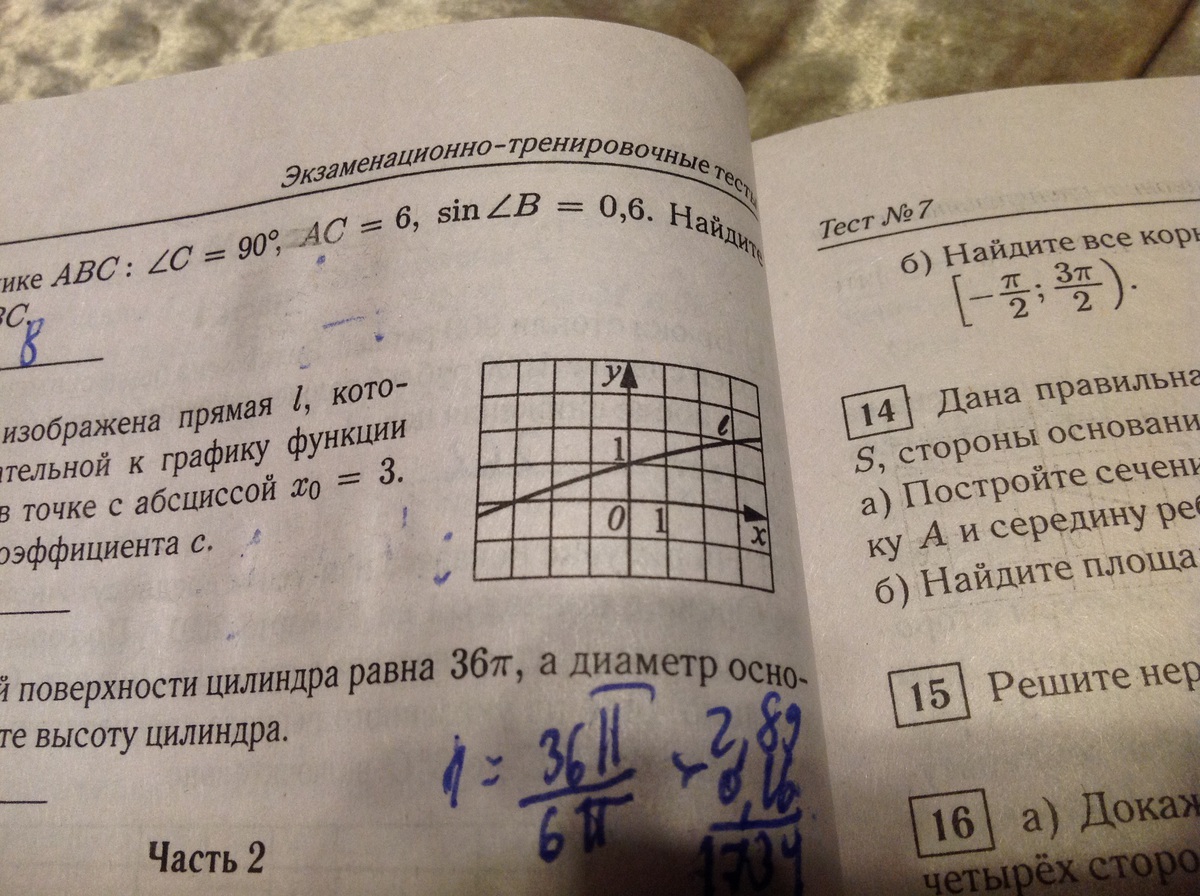
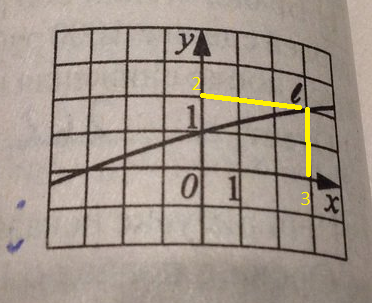
На рисунке изображена прямая l,являющаяся касательной к графику функции y=2x^3+bx+c в точке с абсциссой x=3.Найдите значение коэффициента c
Приложения:
Ответы
Автор ответа:
0
Касательная- это прямая вида у= kx+в
Cм. рисунок в=1
Чтобы найти k подставим координаты точки (3;2) в уравнение
у=kx+1
2=k·3+1 ⇒ 3k=1 k=1/3
Уравнение касательной у=(1/3)х +1
Геометрический смысл производной
f`(x₀)=k( касательной)
f`(x)=(2х³+bx+c)`=6x²+b
f`(3)=6·3²+b
1/3=54+b ⇒ b= 53 целых 2/3
Точка касания (3;2) принадлежит и касательной и кривой
Подставляем её координаты в уравнение кривой
2=2·3³+(53 целых 2/3)·3 + с
2=54+161+с ⇒ с=213
Cм. рисунок в=1
Чтобы найти k подставим координаты точки (3;2) в уравнение
у=kx+1
2=k·3+1 ⇒ 3k=1 k=1/3
Уравнение касательной у=(1/3)х +1
Геометрический смысл производной
f`(x₀)=k( касательной)
f`(x)=(2х³+bx+c)`=6x²+b
f`(3)=6·3²+b
1/3=54+b ⇒ b= 53 целых 2/3
Точка касания (3;2) принадлежит и касательной и кривой
Подставляем её координаты в уравнение кривой
2=2·3³+(53 целых 2/3)·3 + с
2=54+161+с ⇒ с=213
Приложения:
Автор ответа:
0
b = - 53 целых 2/3
, тогда с=109
, тогда с=109
Автор ответа:
0
2=54-161+с
Автор ответа:
0
Да,верно,спасибо
Похожие вопросы
Предмет: Математика,
автор: anaraibraeva315
Предмет: Химия,
автор: Аноним
Предмет: Информатика,
автор: Аноним
Предмет: История,
автор: nastya1112223334444