Question

Прямая АВ касается окружности с центром в точке О и радиусом,равным 9 см,в точке В. Найдите АВ, если АО = 41 см.

К окружности с центром в точке О из точки А проведыны две касательные, угол между которыми равен 60°.Найдите радиу с окружностью, если ОА = 16 см.

К окружности с центром в точке О и радиусом 6 см из точки А проведены две касательные. Найдите угол между этими касательными, если ОА = 4 под корнем 3

Вершина А прямоугольника АВСD является центром окружности радиуса АВ. Докажите, чо прямая ВС являетс касательной к данной окружности.

 

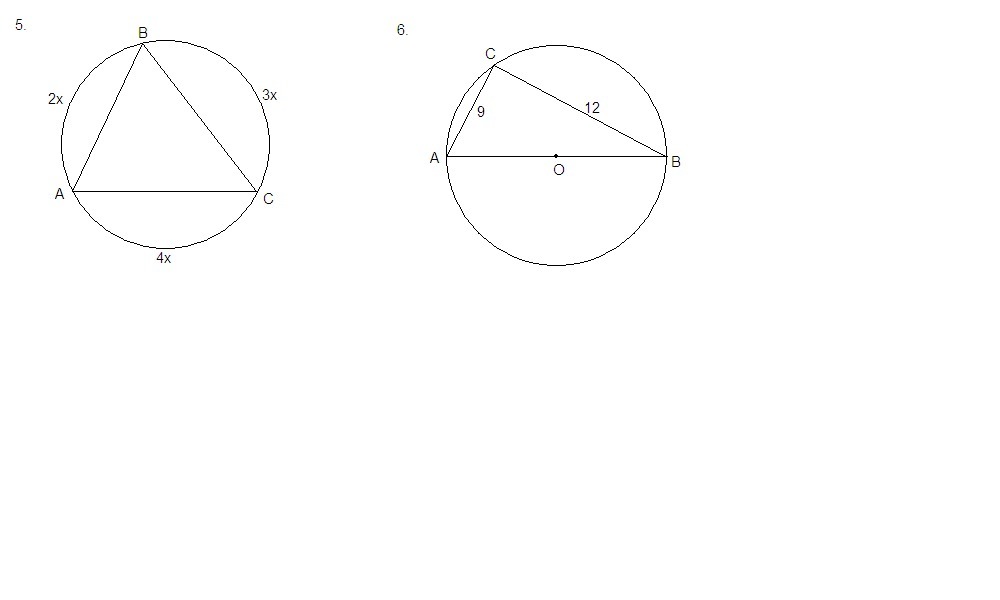
Вершины треугольника АВС делят окружность в отношении 2:3:4. Найдите углы этого треугольника.

Расстояние от точки до концов диаметра равны 9 см и 12 см. Найдите радиус окружности.

 

 

Answer 1

1. Радиус, проведенный в точку касания, перпендикулярен касательной, значит ОВ⊥АВ.
Из ΔАОВ по теореме Пифагора
АВ = √(41² - 9²) = √((41 - 9)(41 + 9)) = √(32 · 50) = √1600 = 40 см

2.  Проведем радиусы ОВ и ОС в точки касания.
Тогда ∠АВО = ∠АСО = 90°, ОВ = ОС как радиусы, ОА - общая гипотенуза для треугольников АВО  и АСО, ⇒
ΔАВО = ΔАСО по катету и гипотенузе.
Значит, ∠ВАО = ∠САО = 1/2 ∠ВАС = 1/2 · 60° = 30°.
В прямоугольном треугольнике АОС ОС - катет, лежащий напротив угла в 30°, значит он равен половине гипотенузы:
R = OC = 1/2AO = 8 см

3. В прямоугольном треугольнике  АОС
sin∠САО = OC/OA = 6 / (4√3) = 3√3 / 6 = √3/2
Значит ∠САО = 60°.
Так как ∠ВАО = ∠САО (доказано в предыдущей задаче), то
∠ВАС = 120°.

4. АВ⊥ВС как стороны прямоугольника, значит АВ - расстояние от точки А  - центра окружности - до прямой ВС. Это расстояние равно радиусу, значит прямая ВС - касательная к окружности.

5.  Пусть х - коэффициент пропорциональности. Тогда соответствующие дуги окружности равны 2х, 3х и 4х. В сумме они составляют 360°.
2x + 3x + 4x = 360°
9x = 360°
x = 40°
Вписанный угол равен половине дуги, на которую опирается.
∪АВ = 80°, ⇒ ∠С = 40°,
∪ВС = 120°, ⇒ ∠А = 60°,
∪АС = 160°, ⇒ ∠В = 80°.

6. Неточное условие. Должно быть так:
Расстояния от точки окружности до концов диаметра равны 9 см и 12 см. Найдите радиус окружности.
Вписанный угол АСВ опирается на диаметр, значит он прямой.
Из прямоугольного треугольника по теореме Пифагора
АВ = √(АС² + ВС²) = √(81 + 144) = √225 = 15 см
R = 1/2AB = 7,5 см