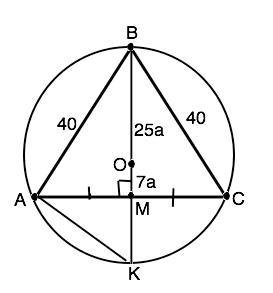
Центр окружности, описанной около равнобедренного треугольника, делит медиану, проведенную к основанию, в отношении 25:7. Боковая сторона треугольника равна 40 см. Найдите радиус окружности, вписанной в треугольник.
Ответы
Ответ: r=12 см
Объяснение: Обозначим данный треугольник АВС, ВМ - медиана, О - центр описанной окружности, ВК - диаметр.
Медиана равнобедренного треугольника к основанию является его высотой и биссектрисой.⇒ ВМ⊥АС.
Примем коэффициент отношения отрезков медианы равным а. Тогда ВО=25а, ОМ=7а.
∠КАВ – вписанный, ВК - диаметр, ⇒ ∆ ВАК прямоугольный, АМ - его высота. Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.⇒ АМ²=КМ•ВМ.
ОК=ОВ=25а - радиусы. ⇒ ВМ=ВО+ОМ=25а+7а=32а; МК= ОК-ОМ=25а-7а=18а. ⇒ АМ²=32а•18а=576а², откуда AM=√576a²=24a.
Из прямоугольного ∆ АВМ по т.Пифагора АМ²+ВМ²=АВ², т.е. 24а²+32а*=1600, откуда а=1 см.
Формула радиуса вписанной в треугольник окружности r=S/p, где Ѕ - площадь треугольника. р - его полупериметр. r=0,5•ВМ•АС:0,5(АВ+ВС+АС)=12 см