Предмет: Алгебра,
автор: Kasumi210
Помогите решить неравенство,пожалуйста
Приложения:
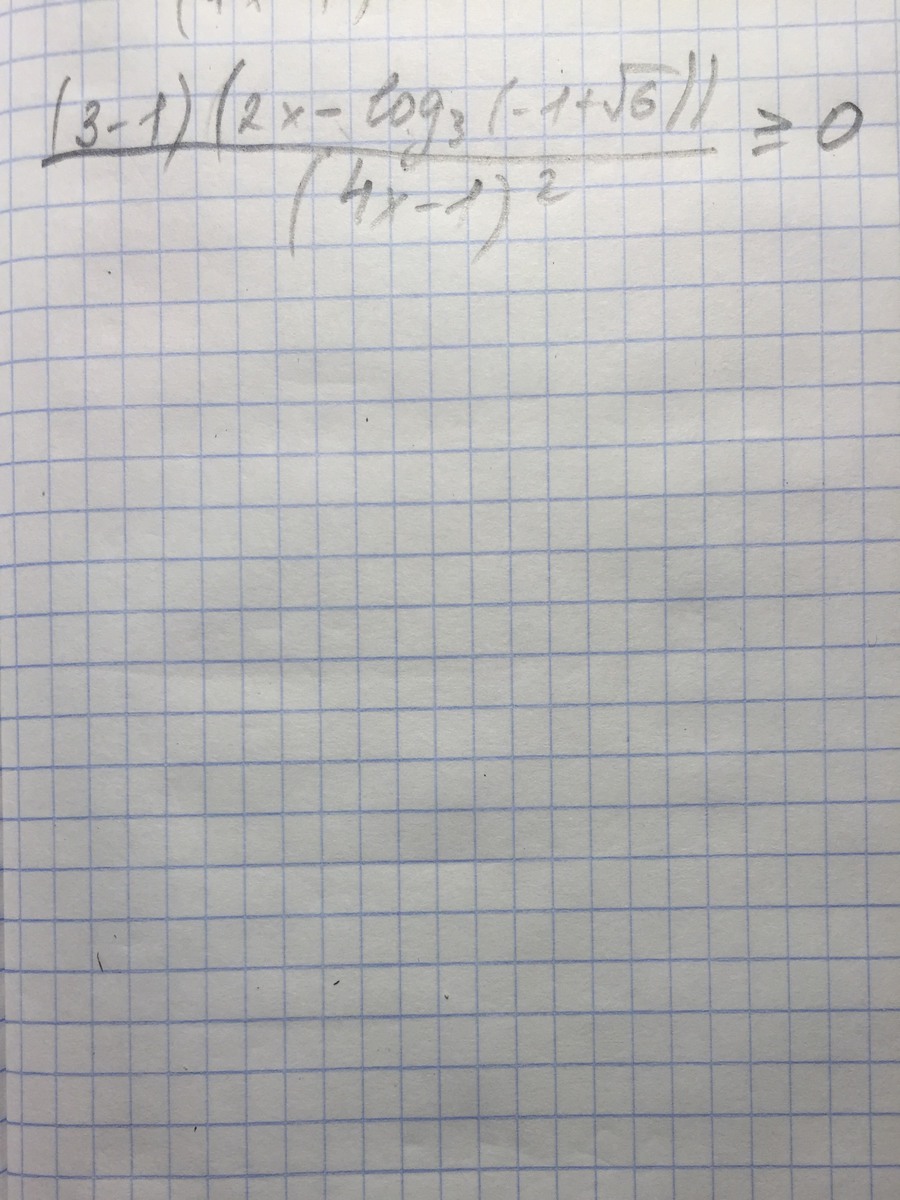
Ответы
Автор ответа:
0
Автор ответа:
0
2 > 0,
с учетом допустимых значений (4x-1)² > 0,
поэтому данное неравенство равносильно следующему
используя метод рационализации, переходим к равносильному неравенству:
Автор ответа:
0
И зачем метод рационализации здесь ? И так всё получается простейшим образом.
Похожие вопросы
Предмет: Геометрия,
автор: margarita5761
Предмет: Математика,
автор: maksim57943
Предмет: Математика,
автор: klaramarat9698
Предмет: Математика,
автор: Anna051rka