Предмет: Алгебра,
автор: filimonov2212
найдите наименьшее значение функции y=sqrt(x^2+12x+40)
Ответы
Автор ответа:
0
Автор ответа:
0
D(y) x∈R
Проверим является ли точка x=-6 точкой минимума (картинка 1)
__
Подставим
Ответ: наименьшее значение функции 2
Приложения:
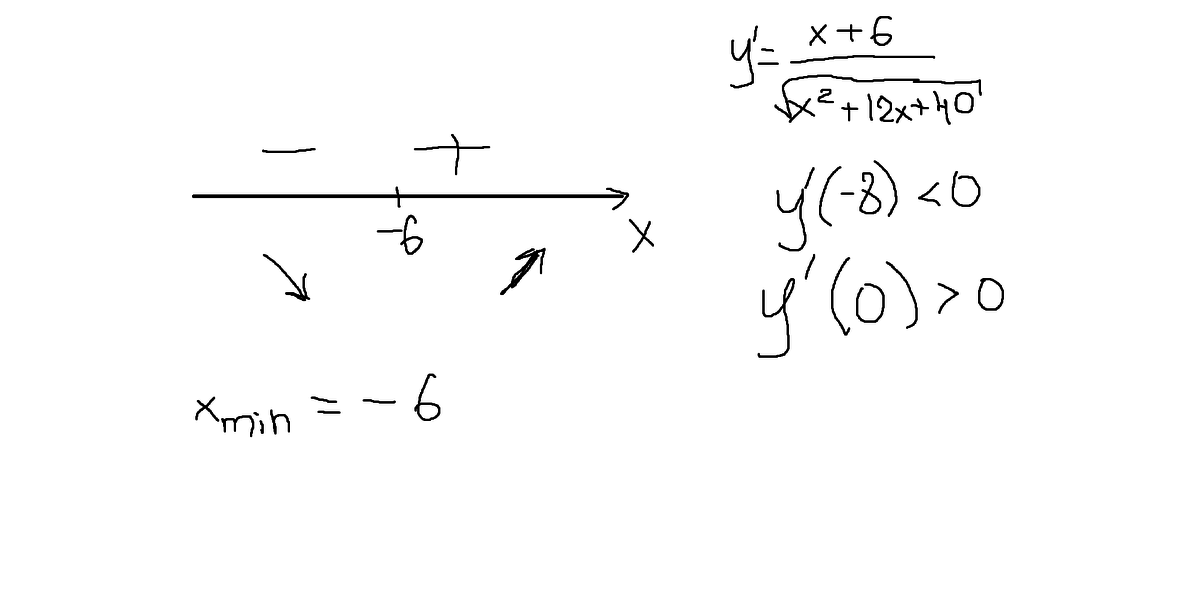
Похожие вопросы
Предмет: Английский язык,
автор: timofejtarasenko93
Предмет: Литература,
автор: NikeTheNight
Предмет: Английский язык,
автор: aleksadasha
Предмет: Математика,
автор: zvorigina
Предмет: Математика,
автор: mohrujon