Question

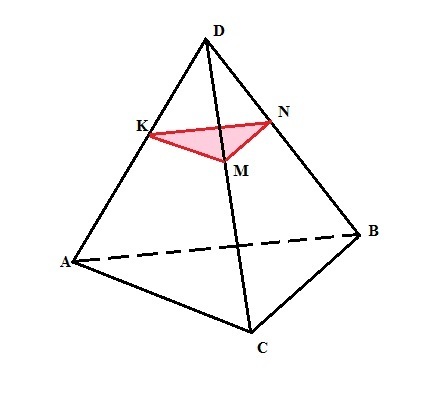
через точку K на ребре АD тетраэдра DABC проведено сечение параллельно грани равна АВС площадь сечения равна 27,АК:КД=1:3.НАЙДИТЕ ПЛОЩАДЬ ГРАНИ АВС

Answer 1

Пусть проведенное сечение пересекает ребра тетраэдра DC и DB в точках M и N соответственно. Значит сечение представляет собой треугольник KMN, параллельный треугольнику АВС и подобен ему в силу параллельности их соответственных сторон. 

Рассмотрим треугольники DKM и DAC. Они подобны, так как КМ║АС. АК:КD=1:3. AK=x, тогда KD=3х. АD=AK+KD = 4x.KD/AD=3/4. Это коэффициент подобия треугольников. Итак, КМ/АС=3/4. => это коэффициент подобия треугольников KMN и АВС. 

Площади подобных фигур относятся как квадрат коэффициента подобия этих фигур, то есть Skmn/Sabc=(3/4)² и Sabc=16*Skmn/9 = 16*27/9 = 48 ед². 

Ответ: Sabc=48 ед².