Предмет: Алгебра,
автор: dexi1ter
Знайти інтеграли, будь-ласка хто може, буду дуже вдячний
Приложения:
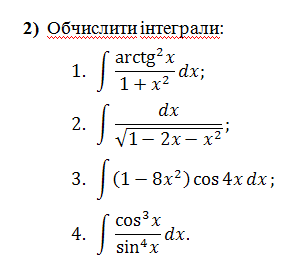
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: dzalilovarushana
Предмет: Алгебра,
автор: aidinanurbekova3
Предмет: Қазақ тiлi,
автор: svetlanakruglik31
Предмет: Математика,
автор: Малая123456
Предмет: Геометрия,
автор: alenaASD