Предмет: Алгебра,
автор: Sten1999
Решите уравнение:
log2(2x-1)-2=log2(x+2)-log2(x+1)
Распишите полностью, пожалуйста.
Ответы
Автор ответа:
0
________________________________
Решено при помощи свойства логарифмов с учётом О. Д. З.

ОТВЕТ: 3
Решено при помощи свойства логарифмов с учётом О. Д. З.
ОТВЕТ: 3
Приложения:
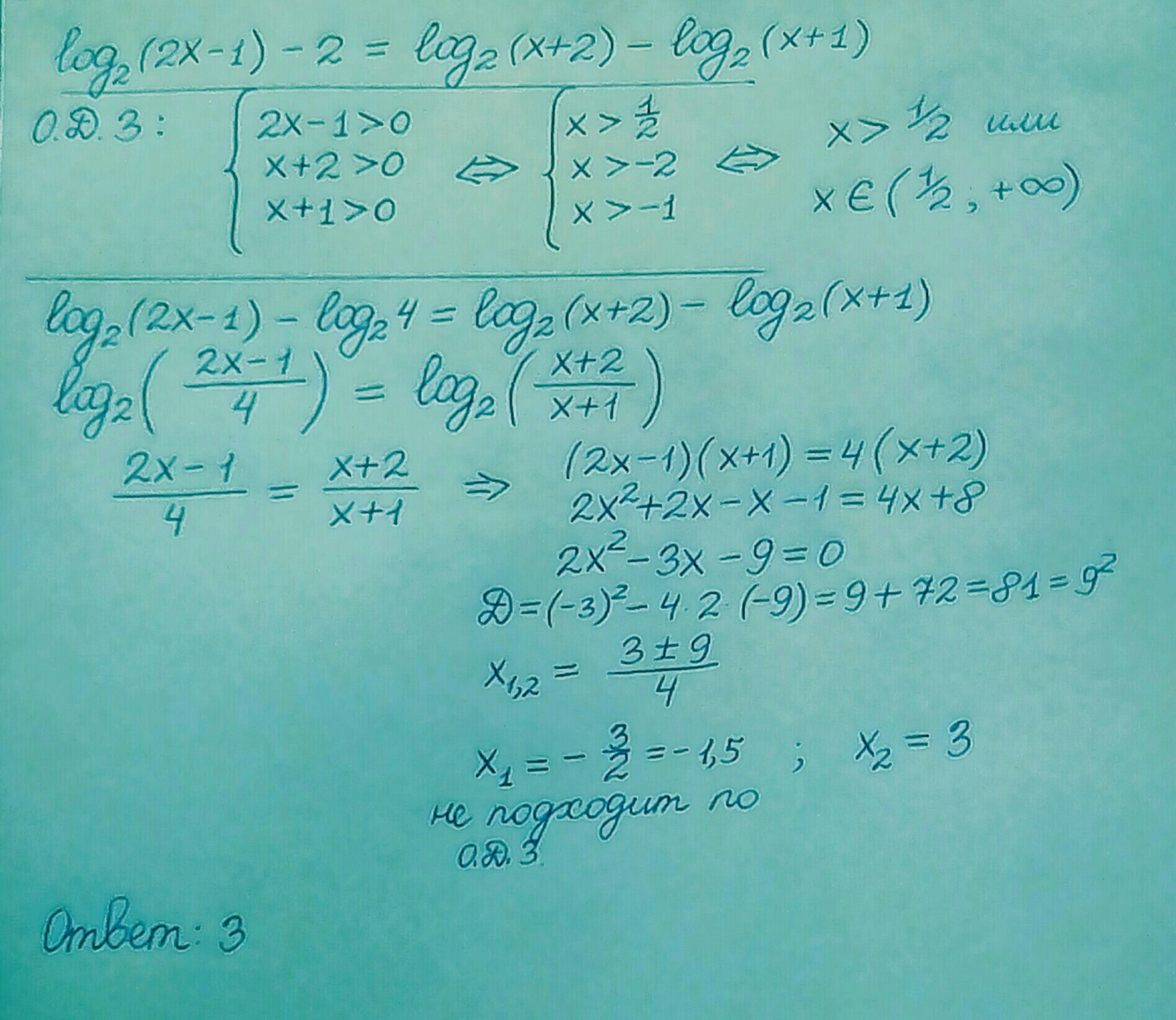
Автор ответа:
0
(2x - 1)(x + 1) = 4(x + 2)
2x² + 2x -x - 1 = 4x + 8
2x² - 3x - 9 = 0
D = 9 + 4*2*9 = 81 = 9²
x₁ = (3 - 9)/4 = -1,5
x₂ = (3 + 9)/4 = 3
Проверка корней
1) x₁ = -1,5 - не подходит по ОДЗ логарифма :
2) x₂ = 3
Ответ : x = 3
Приложения:
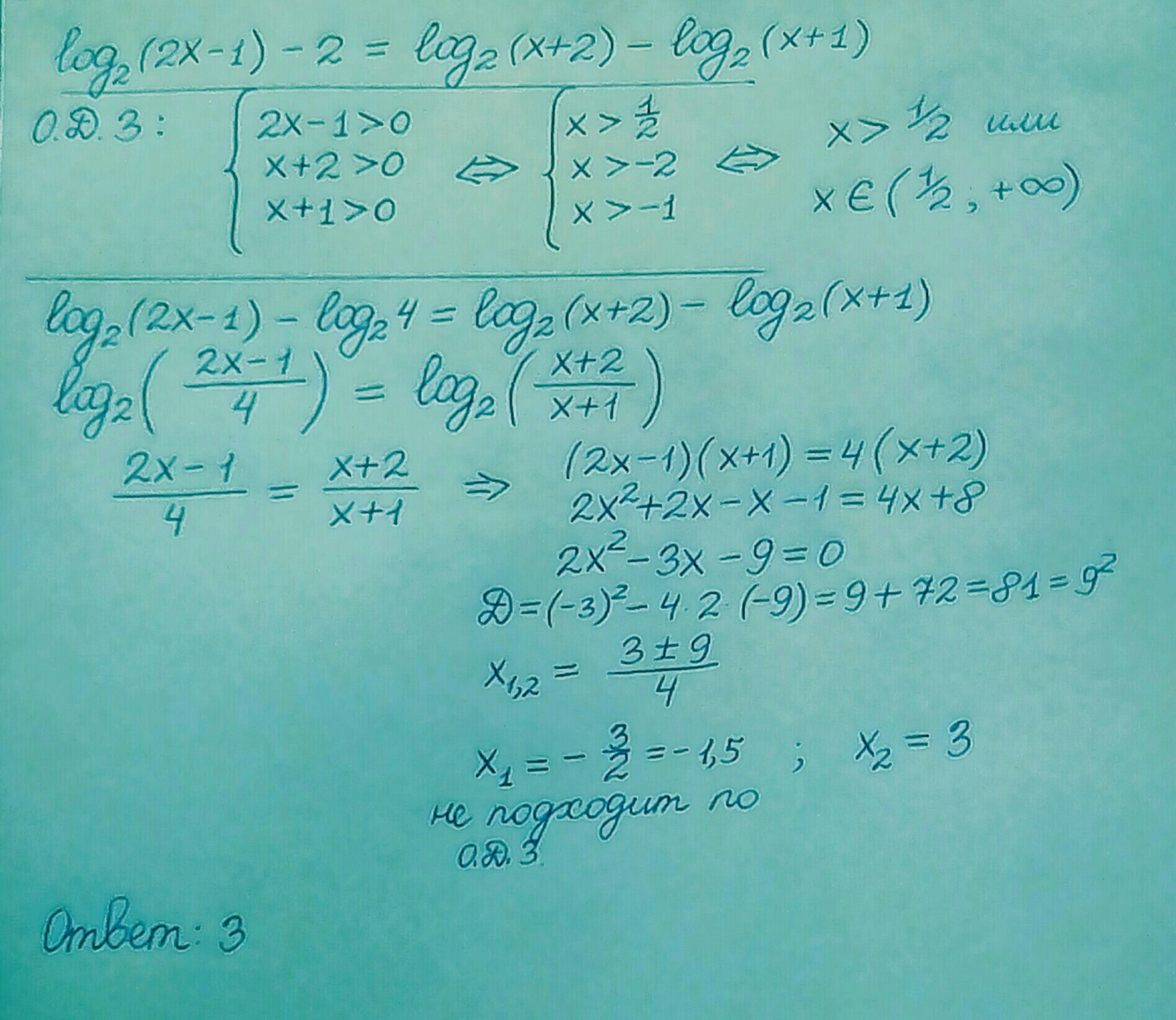
Похожие вопросы
Предмет: Математика,
автор: vibika986
Предмет: Українська мова,
автор: tambov227
Предмет: Литература,
автор: polinapdd
Предмет: Математика,
автор: Аноним