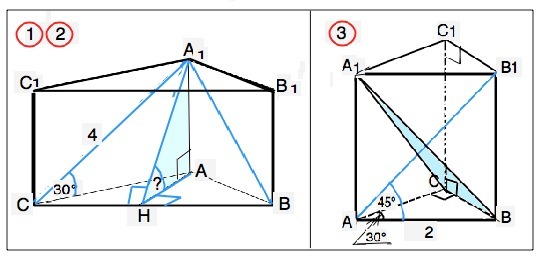
1) В правильной треугольной призме ABCA1B1C1 угол А1СА=30, А1С=4см, найдите тангенс угла между плоскостями А1ВС и АВС
2) Используя условие задания 1 найдите площадь треугольника А1ВС
3)В основании прямой призмы АВСА1В1С1 - треугольник АВС, у которого угол С=90, АВ=2, угол ВАС=30, угол В1АВ=45. Найдите площадь треугольника А1СВ
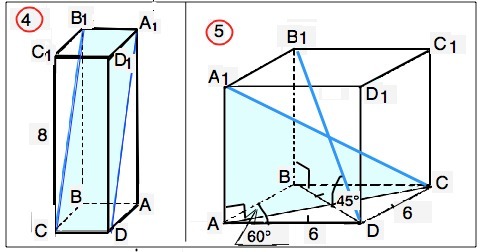
4) Площадь основания правильной призмы ABCDA1B1C1D1 равна 1.5 см в квадрате, высота призмы равна 8 см, найдите площадь сечения A1B1CD
5) В основании прямой призмы лежит ромб со стороной 6 см и углом 60 градусов. Меньшая диагональ призмы наклонена к основанию под углом 45 градусов. Найдите длину большей диагонали.
Люди помогите срочно пожалуйста
Ответы
1. В призме ABCA1B1C1 основания - равносторонние треугольники, а боковые грани - прямоугольники, перпендикулярные основаниям. Угол между плоскостями АВС и А1ВС равен линейному углу между прямыми, проведенными в этих плоскостях перпендикулярно к одной точке на ребре ВС. Это угол А1НА, т.к. высота АН основания призмы перпендикулярна АВ, является проекцией наклонной А1Н. По т.о 3-х перпендикулярах А1Н⊥ВС. ∆ АА1Н - прямоугольный.
А1А =А1С:2=2 см (противолежит углу 30°). АС=А1С•cos30°=2√3 см. АН=АС•sin60°=2√3•√3/2=3 см. tg∠A1AH=2/3
* * *
2. S(CA1B)=A1H•BC:2. A1H=√(AH²+AA1²)=√(2²+3²)=√13. BC=AC=2√3. ⇒ S(CA1B)=0,5•2√3•√3=√39 см²
* * *
3. Данная призма прямая. По условию угол В1АВ=45°⇒ ВВ1=АВ•tg45°=2•1 В ∆ АВС катет ВС=АВ•sin30°=2•1/2=1. Катет АС=АB•cos30°=2•√3/2=√3. Угол АСВ прямой. АС - проекция А1С на плоскость ∆ АСВ. По т. о 3-х перпендикулярах А1С⊥СВ. ⇒ ∆ А1СВ прямоугольный. По т.Пифагора А1С=√(AC²+AA1*)=√((√3)²+2)²=√7. S(A1CB)=0.5•A1C•CB=√7•1=0,5√7
* * *
4. Призма ABCDA1B1C1D1 правильная, ⇒ АВСD - квадрат. АВ=А1В1=√S=√1.5. Ребра данной призмы равны ее высоте. Из прямоугольного СВВ1 по т.Пифагора диагональ боковой грани СВ1=√(BC²+BB1²)=√(1,5+64)=√65,5. S(A1B1CD)=CD•CB1=(√1,5)•(√65,5)=√98,25 ≈ 9,912 см²
* * *
5. Острый угол основания 60° ⇒ меньшая диагональ ромба делит его на два равносторонних, поэтому равна его стороне и является проекцией меньшей диагонали призмы. ВD=6 см. Большая диагональ основания АС равна удвоенной высоте правильного ∆ АВD. АС=2•АВ•sin60°=2•6•(√3/2)=6√3 см.
Угол В1DB=45°⇒ BB1=BD•tg45°=6 см. АА1 перпендикулярна основанию, ⇒ ∆ АА1С - прямоугольный. По т.Пифагора А1С=√(AC²+AA1²)=√(36+108)=√144=12 см