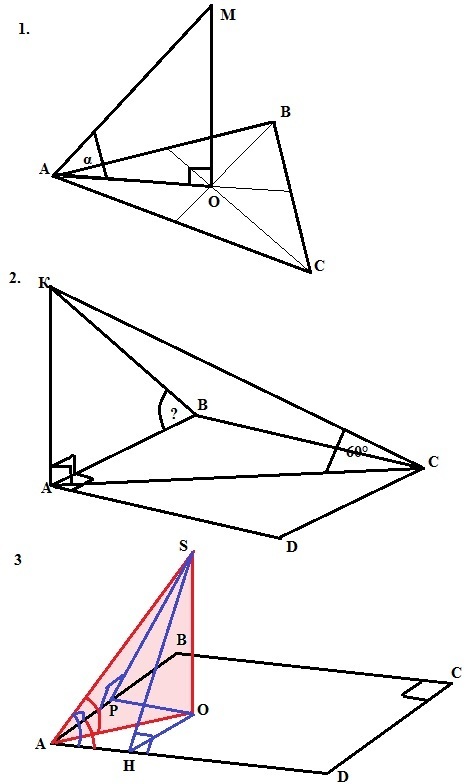
1.медианы правильного треугольника АВС пересекаются в точке О,ОМ перпендикулярно (АВС) ,ОМ=√3 ,АВ=2√3 .Найдите тангенс угла между АМ и плоскостью
треугольника АВС.
2.АВСD-прямоугольник ,КА перпендикулярно (АВС),угол между КС и плоскостью (АВС) равен 60°,АС=5 см ,КВ=11 см.Найдите синус угла между прямой КВ и плоскостью( АВС).
3.Через вершину А прямоугольника АВСD проведена наклонная АS к плоскости прямоугольника,составляющая угол 60° со сторонами АD и АВ.Найдите угол между этой наклонной и плоскостью прямоугольника.
Срочноо!И как можно подробнее!крик души)
Ответы
1. Угол между наклонной к плоскости и плоскостью - это угол между наклонной и ее проекцией на плоскость. Искомый угол - угол МАО. Высота правильного треугольника равна h=(√3/2)*a = (√3/2)*2√3=3. АО=(1/3)*h = 1 (свойство медианы). Tg(<MAO) = MO/AO = √3.
Ответ: α = arctg√3 = 60°
2. Искомый угол - угол между наклонной и ее проекцией, то есть угол АВК. Sin(<ABK) = KA/KB = AC*tg60/5 = 5√3/11. <ABK = arcsin(0,787) ≈ 51,9°.
3. Опустим перпендикуляры SP и SH из точки S к сторонам АВ и АD соответственно. Прямоугольные треугольники APS и AHS равны по гипотенузе и острому углу. Значит АР=АН и АРОН - квадрат. тогда АО = АН*√2 (диагональ квадрата), АS = 2*АН (в треугольнике ASH катет АН лежит против угла 30°, а AS - гипотенуза). Косинус искомого угла (между наклонной AS и плоскостью АВСD, равного отношению проекции наклонной к наклонной) = АО/AS = АН√2/(2*АН) = √2/2.
Ответ: искомый угол равен 45°.