Предмет: Геометрия,
автор: ZayacZnaniy
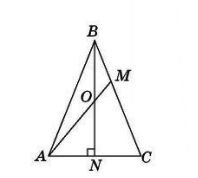
Через вершину А основы АС равнобедренного треугольника АВС проведена прямая, пересекающая высоту треугольника BN и боковую сторону ВС в точках В и М соответственно, причем ВМ: МС = 1: 2. Докажите, что ВО = ON.
Приложения:
Ответы
Автор ответа:
0
треугольник АВС равнобедренный, АВ=ВС, ВН-высота=медиана=биссектриса ВМ/МС=1/2, проводим НК параллельную АМ, по теореме Фалеса АН/НС=МК/КС, АН=НС, 1/1=МК/КС, , т.е МС делится точкой К на две равные части МК=КС=1 часть, и тогда МК=КС=1 часть=ВМ, треугольник ВНК НК паралельна ОМ, по той же теореме, ВМ/МК=ВО/ОН, 1/1=ВО/ОН, 1/1=1/1, т.е т.О делит ВН на две равные части ВО=ОН
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: tenamizabytaa
Предмет: Информатика,
автор: jomartsatai
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: jikdorofeev