Предмет: Алгебра,
автор: Columbus
Решите показательное уравнение! Помогите, оценка решается!!!!!!
Приложения:
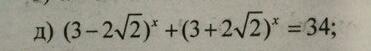
Ответы
Автор ответа:
0
Замена:
Обратная замена:
Похожие вопросы
Предмет: Информатика,
автор: kimjisoo4781
Предмет: Русский язык,
автор: borzakovskaadara
Предмет: Математика,
автор: reginaivanova09
Предмет: Информатика,
автор: verbik
Предмет: Литература,
автор: MaestroGrim