Предмет: Алгебра,
автор: HAppY967
помогите представьте виде многочлена номер 177
Приложения:

Ответы
Автор ответа:
0
Чтобы не было проблем с такими примерами, решим более важную задачу: научимся решать все такие задачи!
Для этого вместе решим аналогичные задачи:
Всё время будем пользоваться двумя строгими правилами, либо для разности, либо для суммы:
 ,
,
 ,
,
где под « A » подразумевается первое слогаемое, а под « x » – второе слогаемое.
Причем это не обязательно просто число или одна буква, это может быть что угодно, даже набор букв и чисел. Надо их просто аккуратно переписывать.
*** 177.1) ;
;
*** 177.3)

 ;
;
*** 177.6)



 ;
;
Для этого вместе решим аналогичные задачи:
Всё время будем пользоваться двумя строгими правилами, либо для разности, либо для суммы:
где под « A » подразумевается первое слогаемое, а под « x » – второе слогаемое.
Причем это не обязательно просто число или одна буква, это может быть что угодно, даже набор букв и чисел. Надо их просто аккуратно переписывать.
*** 177.1)
*** 177.3)
*** 177.6)
Автор ответа:
0
долго еще ?
Автор ответа:
0
решение в приложении.
Приложения:
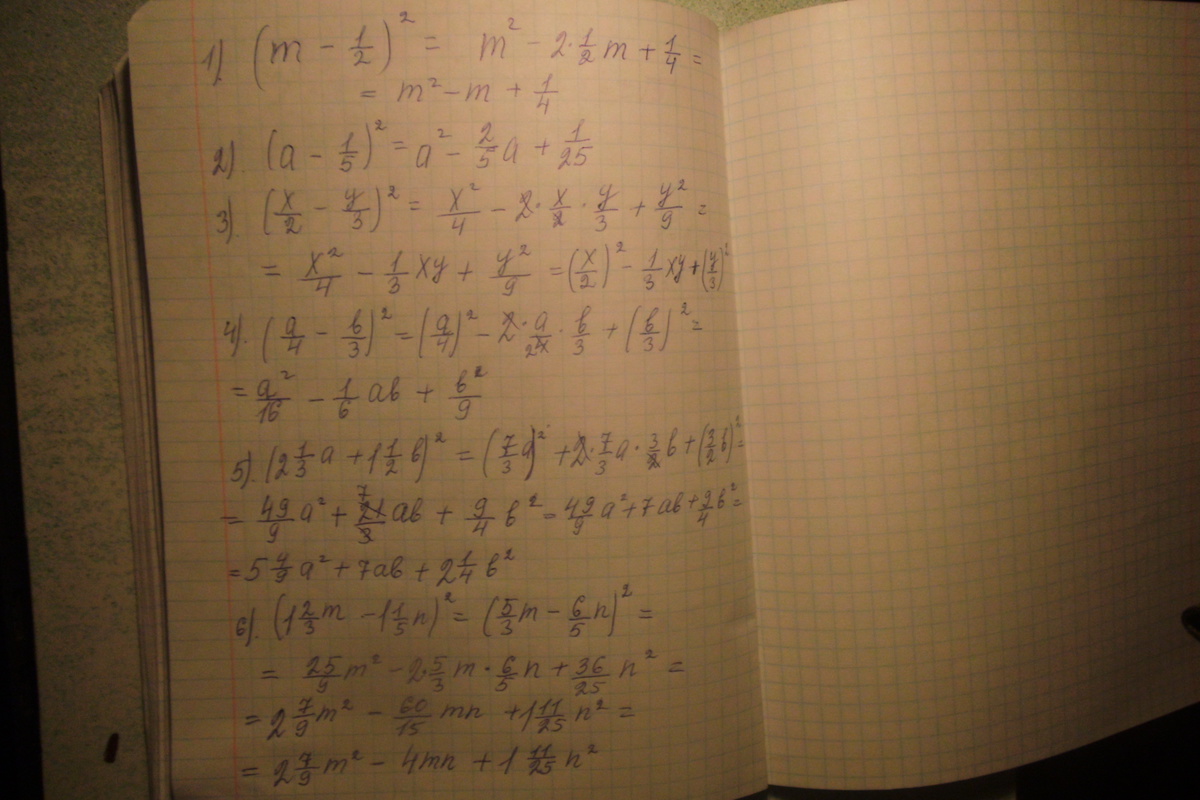
Похожие вопросы
Предмет: Алгебра,
автор: kristinabb69
Предмет: Алгебра,
автор: vikakopycheva
Предмет: Биология,
автор: muminovashaxzoda157
Предмет: Математика,
автор: misabina
Предмет: Алгебра,
автор: lHDlGauSt